
分析 把(-1,0)代入抛物线的解析式求得m=0,得出y=ax2+ax,求得对称轴x=-$\frac{1}{2}$,根据顶点在直线y=x-1上,所以把x=-$\frac{1}{2}$代入y=x-1即可求得顶点坐标,把顶点坐标代入y=ax2+ax,即可求得解析式.
解答 解:∵抛物线y=ax2-a(m-1)x+ma与x轴的交点(-1,0),
∴a+a(m-1)+ma=0,
∴2ma=0,
∵a>0,
∴m=0,
∴抛物线的解析式为y=ax2+ax,
∴对称轴x=-$\frac{1}{2}$,
∵顶点在直线y=x-1上,
∴y=-$\frac{3}{2}$,
∴顶点坐标(-$\frac{1}{2}$,-$\frac{3}{2}$),
∴-$\frac{3}{2}$=$\frac{a}{4}$-$\frac{1}{2}$a,
解得a=6,
∴抛物线的解析式为y=6x2+6x.
点评 本题主要考查了抛物线与x轴的交点以及待定系数法求函数的关系式,解题的关键是求出抛物线的对称轴方程,此题难度不大.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+4x-3交x轴于A、B两点,与y轴交于点C,连AC,点P为第四象限抛物线上一点,且∠PCB=∠ACO,求点P的坐标.
如图,抛物线y=-x2+4x-3交x轴于A、B两点,与y轴交于点C,连AC,点P为第四象限抛物线上一点,且∠PCB=∠ACO,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
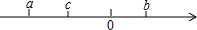 我们知道:正数的绝对值是它本身,不改变前面的符号.负数的绝对值是它的相反数,改变前面的符号.去绝对值符号时,绝对值符号里面如果是几个数的和或差时应加括号.若有理数a、b、c在数轴上的位置如图所示:
我们知道:正数的绝对值是它本身,不改变前面的符号.负数的绝对值是它的相反数,改变前面的符号.去绝对值符号时,绝对值符号里面如果是几个数的和或差时应加括号.若有理数a、b、c在数轴上的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com