
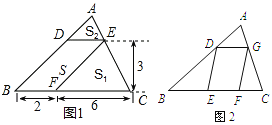
【题目】问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积![]() __________,△ADE的面积
__________,△ADE的面积![]() ______________.
______________.
探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.
【答案】(1)9,1;(2)证明见解析;(3)27.
【解析】
试题分析:本题利用了平行四边形、三角形的面积公式,还利用了平行四边形的判定和性质、相似三角形的判定和性质、平行线分线段成比例定理的推论、全等三角形的判定和性质等知识.
(1)四边形DBFE是平行四边形,利用底×高可求面积;△EFC的面积利用底×高的一半计算;△ADE的面积,可以先过点A作AH⊥BC,交DE于G,交BC于H,即AG是△ADE的高,AH是△ABC的高,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,利用相似三角形的面积比等于相似比的平方,可求AG,再利用三角形的面积公式计算即可;
(2)由于DE∥BC,EF∥AB,可知四边形DBFE是,同时,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,△EFC∽△ABC,从而易得△ADE∽△EFC,利用相似三角形的面积比等于相似比的平方,可得S1:S2=a2:b2,由于S1=![]() bh,那么可求S2,从而易求4S1S2,又S=ah,容易证出结论;
bh,那么可求S2,从而易求4S1S2,又S=ah,容易证出结论;
(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,容易证出△DBE≌△GHF,那么△GHC的面积等于8,再利用(2)中的结论,可求DBHG的面积,从而可求△ABC的面积.
试题解析:(1)S1=9,S2=1;
(2)如图1,
∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴△ADE∽△EFC,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∵S1=![]() bh,
bh,
∴S2=![]() ×S1=
×S1=![]() ,
,
∴4S1S2=4×![]() bh×
bh×![]() =(ah)2,
=(ah)2,
而S=ah,
∴S2=4S1S2;
(3)如图2,过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,
,∴∠GHC=∠B,BD=HG,DG=BH,
∵四边形DEFG为平行四边形,
∴DG=EF,
∴BH=EF,
∴BE=HF,
∴△DBE≌△GHF,
∴△GHC的面积为7+5=12,
由(2)得,平行四边形DBHG的面积S为![]() =12,
=12,
∴△ABC的面积为3+12+12=27.



科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的y与x的部分对应值如表:
X | … | 0 | 1 | 3 | 4 | … |
y | … | 2 | 4 | 2 | ﹣2 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. y最大值为4
C. 当x>1时,y随著x的增大而减小 D. 当0<x<2时,y>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织初三505名学生外出参加社会综合实践活动,现打算租用A、B两种型号的汽车,并且每辆车上都安排1名导游,如果租用这两种型号的汽车各5辆,则刚好坐满;如果全部租用B型汽车,则需13辆汽车,且其中一辆会有2个空位,其余汽车都坐满.(注:同种型号的汽车乘客座位数相同)
(1)求A、B两种型号的汽车分别有多少个乘客座位?
(2)综合考虑多种因素,最后该公司决定租用9辆汽车,问最多安排几辆B型汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE。
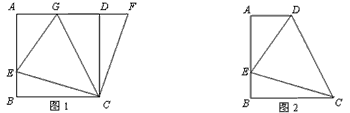
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且
∠DCE=45°,BE=4,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A、B、C是直线l上的三点,P是直线l外一点,且PA=5cm,PB=4cm,PC=3cm,
则点P到直线l的距离 ( )
A. 等于3 cm B. 大于3 cm而小于4 cm ; C. 不大于3 cm D. 小于3 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com