
【题目】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.求证:(1)△ADE≌△CDF;(2)∠BEF=∠BFE.

科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
(1)若点P落在矩形ABCD的边AB上(如图1).
①当点P与点A重合时,∠DEF= °,当点E与点A重合时,∠DEF= °.
②当点E在AB上时,点F在DC上时(如图2),若AP=![]() ,求四边形EPFD的周长.
,求四边形EPFD的周长.
(2)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图3),当AM=DE时,请求出线段AE的长度.

(3)若点P落在矩形的内部(如图4),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线l1:![]() 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2:![]() 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.
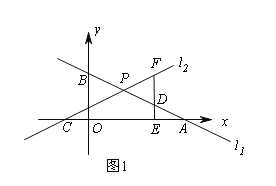
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
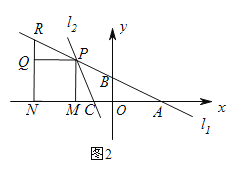
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,(在弹性限度![]() 内)已知一弹簧的长度
内)已知一弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系如下表:
之间的关系如下表:
物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(1)当物体的质量为![]() 时,弹簧的长度是多少?
时,弹簧的长度是多少?
(2)如果物体的质量为![]() ,弹簧的长度为
,弹簧的长度为![]() ,根据上表写出
,根据上表写出![]() 与x的关系式;
与x的关系式;
(3)当物体的质量为![]() 时,求弹簧的长度.
时,求弹簧的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解:
都可以进行这样的分解:![]() (
(![]() 是正整数,且
是正整数,且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解,产规定:
的最佳分解,产规定:![]() ,例如:12可以分解成
,例如:12可以分解成![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 是12的最佳分解,所以
是12的最佳分解,所以![]() .
.
(1)求![]() ;
;
(2)若正整数![]() 是4的倍数,我们称正整数
是4的倍数,我们称正整数![]() 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数![]() ,
,![]() (
(![]() ,
,![]() 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数![]() 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com