
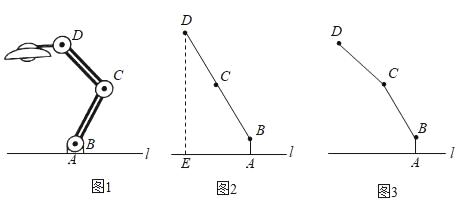
【题目】如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC、CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
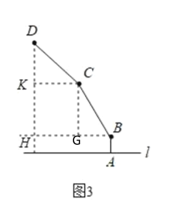
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
【答案】(1)(20![]() +5)cm;(2)比原来降低了(10
+5)cm;(2)比原来降低了(10![]() ﹣10)厘米.
﹣10)厘米.
【解析】
(1)作BO⊥DE于O,根据矩形的判定,可得四边形ABOE是矩形,先求出∠DBO,然后根据锐角三角函数即可求出OD,从而求出DE;
(2)过C作CG⊥BH,CK⊥DE,根据锐角三角函数,即可求出CG,从而求出KH,再求出∠DCK,利用锐角三角函数即可求出DK,从而求出此时连杆端点D离桌面l的高度,即可求出结论.
解:(1)如图2中,作BO⊥DE于O.
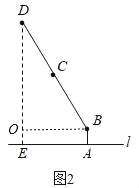
∵∠OEA=∠BOE=∠BAE=90°,
∴四边形ABOE是矩形,
∴∠OBA=90°,
∴∠DBO=150°﹣90°=60°,
∴OD=BDsin60°=20![]() (cm),
(cm),
∴DE=OD+OE=OD+AB=(20![]() +5)cm;
+5)cm;
(2)过C作CG⊥BH,CK⊥DE,
由题意得,BC=CD=20m,CG=KH,
∴在Rt△CGB中,sin∠CBH=![]() ,
,
∴CG=10![]() cm,
cm,
∴KH=10![]() cm,
cm,
∵∠BCG=90°﹣60°=30°,
∴∠DCK=150°﹣90°﹣30°=30°,
在Rt△DCK中,sin∠DCK=![]() =
=![]() =
=![]() ,
,
∴DK=10cm,
∴此时连杆端点D离桌面l的高度为10+10![]() +5=(15+10
+5=(15+10![]() )cm
)cm
∴比原来降低了(20![]() +5)﹣(15+10
+5)﹣(15+10![]() )=10
)=10![]() ﹣10,
﹣10,
答:比原来降低了(10![]() ﹣10)厘米.
﹣10)厘米.


科目:初中数学 来源: 题型:
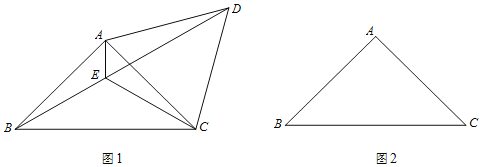
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
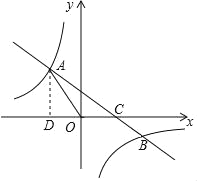
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)点E是x轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=2ax2﹣ax﹣3(a+1)与x轴交于点AB(点A在点B的左侧).
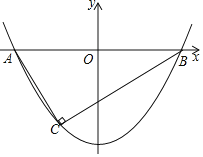
(1)不论a取何值,抛物线总经过第三象限内的一个定点C,请直接写出点C的坐标;
(2)如图,当AC⊥BC时,求a的值和AB的长;
(3)在(2)的条件下,若点P为抛物线在第四象限内的一个动点,点P的横坐标为h,过点P作PH⊥x轴于点H,交BC于点D,作PE∥AC交BC于点E,设△ADE的面积为S,请求出S与h的函数关系式,并求出S取得最大值时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=900,∠BAD=600,对角线AC平分∠BAD,且AB=AC=4,点E、F分别是AC、BC的中点,连接DE,EF,DF,则DF的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点C、D在x轴上,A、B恰好在二次函数y=2x2﹣4的图象上,则图中阴影部分的面积之和为( )
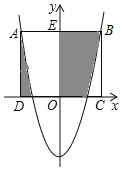
A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:
(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;
(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
根据以上作图过程及所作图形,下列结论中错误的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com