
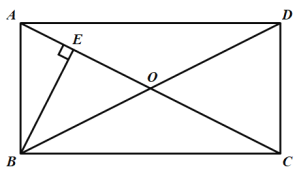
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
(1)求证:![]() ABCD是矩形;
ABCD是矩形;
(2)若AD=![]() ,cos∠ABE=
,cos∠ABE=![]() ,求AC的长.
,求AC的长.
【答案】(1)见解析;(2)5.
【解析】
(1)先说明.OA=OC,OB=OD,再证得AC=BD,即可证明![]() ABCD是矩形;
ABCD是矩形;
(2)先说明∠BAD=∠ADC=90°,再求得∠CAD=∠ABE,最后解直角三角形即可.
(1)证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵OA=OB,
∴OA=OB=OC=OD,
∴AC=BD,
∴![]() OABCD是矩形;
OABCD是矩形;
(2)解∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,
∴∠BAC+∠CAD=90°,
∵BE⊥AC,
∴∠BAC+∠ABE=90°,
∴∠CAD=∠ABE,
在Rt△ACD中,AD=![]() ,cos∠CAD=
,cos∠CAD=![]() =cos∠ABE=
=cos∠ABE=![]()
∴AC=5.


科目:初中数学 来源: 题型:
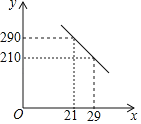
【题目】一名大学毕业生响应国家“自主创业”的号召,在成都市高新区租用了一个门店,聘请了两名员工,计划销售一种产品.已知该产品成本价是20元/件,其销售价不低于成本价,且不高于30元/件,员工每人每天的工资为200元.经过市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)求每件产品销售价为多少元时,每天门店的纯利润最大?最大纯利润是多少?(纯利润=销售收入﹣产品成本﹣员工工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
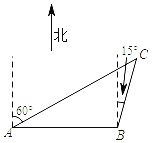
【题目】在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距__千米.(结果精确到0.1千米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2+PB2=PC2,则称点P为△ABC关于点C的勾股点.

(1)如图2,在4×3的方格纸中,每个小正方形的边长均为1,△ABC的顶点在格点上,请找出所有的格点P,使点P为△ABC关于点A的勾股点.
(2)如图3,△ABC为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角三角形APD(点A、P、D顺时针排列)∠PAD=90°,连接DC,DB,求证:点P为△BDC关于点D的勾股点.
(3)如图4,点E是矩形ABCD外一点,且点C是△ABE关于点A的勾股点,若AD=8,CE=5,AD=DE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线L:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数![]() (x>0)的图象的交点P位于第一象限.
(x>0)的图象的交点P位于第一象限.
(1)若点P的坐标为(1,6),
①求m的值及点A的坐标;
②![]() =_________;
=_________;
(2)直线h:y=2kx-2与y轴交于点C,与直线L1交于点Q,若点P的横坐标为1,
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
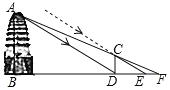
【题目】如图,西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.某周末,小乐和小夏相约去小雁塔游玩,在休息时,他们想利用所学知识测量小雁塔的高度,于是他们向工作人员借来测量工具由于观测点与小雁塔底部间的距离不易测量,于是他们利用太阳光照射影子进行测量,小乐先在小雁塔的影子顶端![]() 处竖直立一根长1.72米的木棒
处竖直立一根长1.72米的木棒![]() ,并测得此时木棒的影长
,并测得此时木棒的影长![]() 米;然后小夏在
米;然后小夏在![]() 的延长线上找出一点
的延长线上找出一点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 三点在同一直线上,并测得
三点在同一直线上,并测得![]() 米已知图中所有点均在同一平面内,
米已知图中所有点均在同一平面内,![]() ,
,![]() ,根据以上测量过程及数据,请你帮他们求出小雁塔的高度
,根据以上测量过程及数据,请你帮他们求出小雁塔的高度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() .
.

(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是
是![]() 轴上的一点,过点
轴上的一点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .横、纵坐标都是整数的点叫做整点.记
.横、纵坐标都是整数的点叫做整点.记![]() 的图象在点
的图象在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点的坐标为______;
内的整点的坐标为______;
②若区域![]() 内恰有6个整点,结合函数图象,求出
内恰有6个整点,结合函数图象,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com