
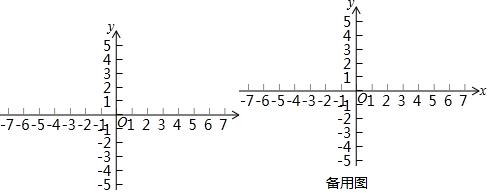
分析 (1)先求出$\frac{3}{2}$r=3,再分别求出OA,OB,OC,OD,再判断即可得出结论;
(2)先求出OE,用圆的“近外点”满足的条件建立不等式组求解即可;
(3)先判断出直线MN中OM>ON,进而得出点M和点G是圆O的“近外点”的分界点,再分两种情况讨论计算.
解答 解:(1)∵⊙O的半径为2,
∴$\frac{3}{2}$r=3,
∵A(4,0),
∴OA=4>3,
∴点A不是⊙O的“近外点”,
B (-$\frac{5}{2}$,0),
∴OB=$\frac{5}{2}$,而2<$\frac{5}{2}$<3,
∴B是⊙O的“近外点”,
C(0,3),
∴OC=3,
∴点C是⊙O的“近外点”,
D (1,-1),
∴OD=$\sqrt{1+1}$=$\sqrt{2}$<2,
∴点D不是⊙O的“近外点”,
故答案为:B,C;
(2)∵E(3,4),
∴OE=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵点E是⊙O的“近外点”,
∴$\left\{\begin{array}{l}{r≤5}\\{\frac{3}{2}r≥5}\end{array}\right.$,
∴$\frac{10}{3}$≤r≤5;
(3)如图,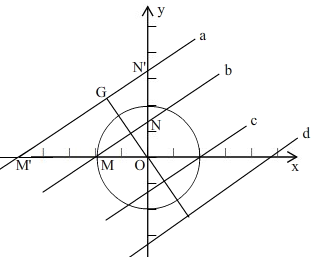
∵直线MN的解析式为y=$\frac{\sqrt{3}}{3}$x+b,
∴OM>ON,
①点N在y轴坐标轴时,
当点M是⊙O的“近外点”,此时,点M(-2,0),
将M(-2,0)代入直线MN的解析式y=$\frac{\sqrt{3}}{3}$x+b中,解得,b=$\frac{2\sqrt{3}}{3}$,
即:b的最小值为$\frac{2\sqrt{3}}{3}$,
过点O作OG⊥M'N'于G,
当点G是⊙O的“近外点”时,此时OG=3,
在Rt△ON'G中,∠ON'G=60°,
∴ON'=$\frac{OC}{sin60°}$=2$\sqrt{3}$,
b的最大值为2$\sqrt{3}$,
∴$\frac{2\sqrt{3}}{3}$≤b≤2$\sqrt{3}$,
②当点N在y轴负半轴时,同①的方法得出,-2$\sqrt{3}$≤b≤-$\frac{2\sqrt{3}}{3}$,
即:$\frac{{2\sqrt{3}}}{3}≤b≤2\sqrt{3}或-2\sqrt{3}≤b≤-\frac{{2\sqrt{3}}}{3}$.
点评 此题是圆的综合题,主要考查了新定义,点到原点的距离的确定,解(2)的关键是利用圆O的“近外点”建立不等式组,解(3)的关键是找出线段MN上的点是圆O的“近外点”的分界点,是一道中等难度的题目.


科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:单选题
抛物线y=- 2x2 - 4x - 5经过平移后得到抛物线y=- 2x2,平移方法是( )
A. 向左平移1个单位,再向下平移3个单位
B. 向左平移1个单位,再向上平移3个单位
C. 向右平移1个单位,再向下平移3个单位
D. 向右平移1个单位,再向上平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
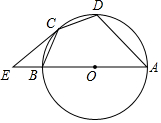 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
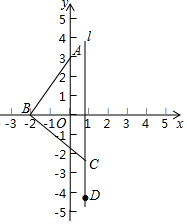 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.
如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
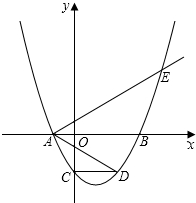 如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),
如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G
在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com