练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．已知二次根式$\sqrt{2{x}^{2}+7}$的值为5，求x的值．

    分析 根据解无理方程，可得答案．

    解答 解：由题意，得
    $\sqrt{2{x}^{2}+7}$=5，
    两边平方，得
    2x2+7=25，
    解得x=±3，
    即x1=3，x2=-3．

    点评 本题考查了二次根式的性质，利用平方解无理方程是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．我校为了纪念“一二•九”举办了八年级红歌合唱比赛，为了保证这次比赛的公正性，规定：参赛班级的基本素养、精神面貌、服装三项打分分别按5：3：2的比例计入总评成绩．二班、三班、五班的基本素养、精神面貌、服装的打分如下表，计算哪个班是第一名？
    基本素养精神面貌服装
    二班909693
    三班909096
    五班969490

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．从-1，0，1，2，3这5个数中，随机抽取一个数记为a，使得二次函数y=2x2-4x-1当x＞a时，y随x 的增大而增大，且使关于x的分式方程$\frac{1-ax}{x-2}$+2=$\frac{1}{2-x}$有整数解的概率为$\frac{1}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

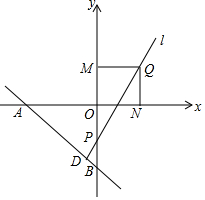    7．如图，在平面直角坐标系中，A（-8，0），B（0，-8），D为直线AB上一点，且D点横坐标为-2，y轴上有一动点P，直线l经过D、P两点．
    （1）求直线AB的表达式和D点坐标；
    （2）当∠ADP=75°时，求点P坐标；
    （3）在直线l上取点Q（Q点位于第一象限，且横、纵坐标之积恰为12），现过点Q作QM⊥y轴于M，QN⊥x轴于N．问：是否存在点P，使得直线DQ分长方形ONQM为两部分，其中所分成的三角形面积是△PDB面积的一半．若存在，直接写出P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解下列方程：
    （1）$\frac{2}{3}$x-1=$\frac{1}{2}$x+3；
    （2）5（x-5）+2（x-12）=0；
    （3）4x+3=2（x-1）+1；
    （4）y+$\frac{1}{2}$=$\frac{2-y}{3}$；
    （5）$\frac{2}{7}$（3x+7）=2-$\frac{3}{2}$x；
    （6）$\frac{2x+5}{6}$-$\frac{3x-2}{8}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．正五边形的画法通常是先把圆分成五等份，然后连接五等分点而得，这种画法的理论依据应（　　）
    A．把圆n等分，顺次连接各分点得到的多边形是圆的内接正n边形
    B．把圆n等分，依次过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形
    C．各边相等．并且各角也相等的多边形是正多边形
    D．用量角器等分圆是一种简单而常用的方法

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．求函数y=$\frac{3{x}^{2}+x+2}{{x}^{2}+2x+1}$的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知：$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=2}\end{array}\right.$和$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$是一次函数y=kx+b的两组对应值．
    （1）求这个一次函数；
    （2）画出这个函数的图象，并求出它与x轴的交点、与y轴的交点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知函数y=ax2+bx+c过点（1，0），（-3，0）和（3，6），则a=$\frac{1}{2}$，b=1，c=-$\frac{3}{2}$．

    查看答案和解析>>

    同步练习册答案