
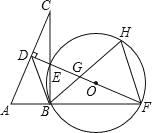
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
【答案】(1)见试题解析;(2)BD与⊙O相切,理由见试题解析;(3)HGHB=2+![]() .
.
【解析】
试题分析:(1)由垂直的定义可得∠EBF=∠ADF=90°,于是得到∠C=∠BFE,从而证得△ABC≌△EBF;
(2)BD与⊙O相切,如图1,连接OB证得∠DBO=90°,即可得到BD与⊙O相切;
(3)如图2,连接CF,HE,有等腰直角三角形的性质得到CF=![]() BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF=
BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF=![]() BF,求得BF=
BF,求得BF=![]() +1,有勾股定理解出EF=
+1,有勾股定理解出EF=![]() =
=![]() ,推出△EHF是等腰直角三角形,求得HF=
,推出△EHF是等腰直角三角形,求得HF=![]() EF=
EF=![]() ,通过△BHF∽△FHG,列比例式即可得到结论.
,通过△BHF∽△FHG,列比例式即可得到结论.
试题解析:(1)证明:∵∠ABC=90°,∴∠EBF=90°,∵DF⊥AC,∴∠ADF=90°,
∴∠C+∠A=∠A+∠AFD=90°,∴∠C=∠BFE,
在△ABC与△EBF中, ,∴△ABC≌△EBF;
,∴△ABC≌△EBF;
(2)BD与⊙O相切,如图1,连接OB
证明如下:∵OB=OF,∴∠OBF=∠OFB,∵∠ABC=90°,AD=CD,∴BD=CD,
∴∠C=∠DBC,∵∠C=∠BFE,∴∠DBC=∠OBF,∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,
∴∠DBO=90°,∴BD与⊙O相切;
(3)解:如图2,连接CF,HE,∵∠CBF=90°,BC=BF,∴CF=![]() BF,
BF,
∵DF垂直平分AC,∴AF=CF=AB+BF=1+BF=![]() BF,∴BF=
BF,∴BF=![]() ,
,
∵△ABC≌△EBF,∴BE=AB=1,∴EF=![]() =
=![]() ,
,
∵BH平分∠CBF,∴![]() ,∴EH=FH,∴△EHF是等腰直角三角形,
,∴EH=FH,∴△EHF是等腰直角三角形,
∴HF=![]() EF=
EF=![]() ,∵∠EFH=∠HBF=45°,∠BHF=∠BHF,∴△BHF∽△FHG,
,∵∠EFH=∠HBF=45°,∠BHF=∠BHF,∴△BHF∽△FHG,
∴![]() ,∴HGHB=HF2=2+
,∴HGHB=HF2=2+![]() .
.




 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 长方体、正方体都是棱柱 B. 三棱柱的侧面是三角形
C. 直六棱柱有六个侧面、侧面为长方形 D. 球体的三种视图均为同样大小的图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“遵义地区明天降水概率是15%”,下列说法中,正确的是( )
A. 遵义地区明天降水的可能性较小
B. 遵义地区明天将有15%的时间降水
C. 遵义地区明天将有15%的地区降水
D. 遵义地区明天肯定不降水
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com