
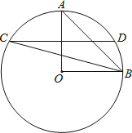
【题目】如图,OA.OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C.D,连接CB.AB.
求证:∠ABC=2∠CBO.
【答案】证明见解析.
【解析】
试题分析:连接OC.AC,如图,根据线段垂直平分线的性质得OC=AC,则可判断△OAC是等边三角形,所以∠AOC=60°,于是根据圆周角定理得到∠ABC=![]() ∠AOC=30°,然后在△BOC中,由于∠BOC=∠AOC+∠AOB=150°,根据三角形内角和可计算出∠CBO=15°,所以∠ABC=2∠CBO.
∠AOC=30°,然后在△BOC中,由于∠BOC=∠AOC+∠AOB=150°,根据三角形内角和可计算出∠CBO=15°,所以∠ABC=2∠CBO.
试题解析:连接OC.AC,如图,
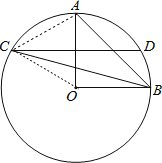
∵CD垂直平分OA,
∴OC=AC.
∴OC=AC=OA,
∴△OAC是等边三角形,
∴∠AOC=60°,
∴∠ABC=![]() ∠AOC=30°,
∠AOC=30°,
在△BOC中,∠BOC=∠AOC+∠AOB=150°,
∵OB=OC,
∴∠CBO=15°,
∴∠ABC=2∠CBO.


科目:初中数学 来源: 题型:
【题目】某股票经纪人给他的投资者出了一道题,说明投资人的赢利净赚情况(单位:元):
股票名称 | 中国重工 | 五粮液 | 工商银行 | 四川路桥 |
每股净赚(元) | +23 | +1.5 | ﹣3 | ﹣(﹣2) |
股数 | 500 | 1000 | 1000 | 500 |
请你计算一下,投资者到底是赔了还是赚了,赔了或赚了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与直线y=x+c的交点的横坐标为1,根据图象有下列四个结论:①a<0;②c>0;③对于直线y=x+c上任意两点A(xA,yA)、B(xB,yB),若xA<xB,则yA>yB;④x>1是不等式ax+b<x+c的解集,其中正确的结论是( )
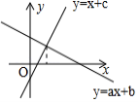
A. ①②B. ①③C. ①④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校在“我和我的祖国”快闪拍摄活动中,为学生化妆.其中5名男生和3名女生共需化妆费190元;3名男生的化妆费用与2名女生的化妆费用相同.
(1)求每位男生和女生的化妆费分别为多少元;
(2)如果学校提供的化妆总费用为2000元,根据活动需要至少应有42名女生化妆,那么男生最多有多少人化妆.
查看答案和解析>>
科目:初中数学 来源: 题型:
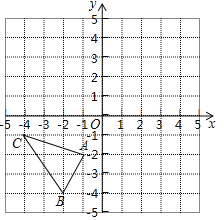
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com