
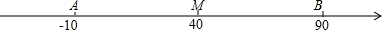
·ÖĪö £Ø1£©Ēó-10Óė90ŗĶµÄŅ»°ė¼“ŹĒM£»
£Ø2£©ĻČĒó³öABµÄ³¤£¬ŌŁÉčtĆėŗóP”¢QĻąÓö¼“æÉµĆ³ö¹ŲÓŚtµÄŅ»ŌŖŅ»“Ī·½³Ģ£¬Ēó³ötµÄÖµ£¬æÉĒó³öP”¢QĻąÓöŹ±µćQŅĘ¶ÆµÄ¾ąĄė£¬½ų¶ųæÉµĆ³öCµć¶ŌÓ¦µÄŹż£»
£Ø3£©·ÖĪŖ2Ö»µē×ÓĀģŅĻĻąÓöĒ°Ļą¾ą35øöµ„Ī»³¤¶ČŗĶĻąÓöŗóĻą¾ą35øöµ„Ī»³¤¶Č£¬ĻąÓöĒ°£ŗ£Ø100-35£©”Ā£Ø2+3£©=13£ØĆė£©£¬ĻąÓöŗó£ŗ£Ø35+100£©”Ā£Ø2+3£©=27£ØĆė£©£®
½ā“š ½ā£ŗ£Ø1£©Mµć¶ŌÓ¦µÄŹżŹĒ£Ø-10+90£©”Ā2=40£»
£Ø2£©”ßA”¢B·Ö±šĪŖŹżÖįÉĻµÄĮ½µć£¬Aµć¶ŌÓ¦µÄŹżĪŖ-10£¬Bµć¶ŌÓ¦µÄŹżĪŖ90£¬
”ąAB=90+10=100£¬
ÉčtĆėŗóP”¢QĻąÓö£¬
”ą3t+2t=100£¬½āµĆt=20£»
”ą“ĖŹ±µćQ×ß¹żµÄĀ·³Ģ=2”Į20=40£¬
”ą“ĖŹ±Cµć±ķŹ¾µÄŹżĪŖ-10+40=30£®
“š£ŗCµć¶ŌÓ¦µÄŹżŹĒ30£»
£Ø3£©ĻąÓöĒ°£ŗ£Ø100-35£©”Ā£Ø2+3£©=13£ØĆė£©£¬
ĻąÓöŗó£ŗ£Ø35+100£©”Ā£Ø2+3£©=27£ØĆė£©£®
Ōņ¾¹ż13Ćė»ņ27Ćė£¬2Ö»µē×ÓĀģŅĻŌŚŹżÖįÉĻĻą¾ą35øöµ„Ī»³¤¶Č£®
µćĘĄ “ĖĢāæ¼²éŅ»ŌŖŅ»“Ī·½³ĢŹ½ĪŖŹµ¼ŹŌĖÓĆ£¬ĄūÓĆŠŠ³ĢĪŹĢāµÄ»ł±¾ŹżĮæ¹ŲĻµ£¬ŅŌ¼°ŹżÖįÖ±¹Ū½ā¾öĪŹĢā¼“æÉ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
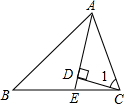 ČēĶ¼£¬ADĘ½·Ö”ĻBAC£¬CD”ĶAD£¬“¹×ćĪŖD£¬ĒóÖ¤£ŗ”Ļ1£¾”ĻB£®
ČēĶ¼£¬ADĘ½·Ö”ĻBAC£¬CD”ĶAD£¬“¹×ćĪŖD£¬ĒóÖ¤£ŗ”Ļ1£¾”ĻB£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
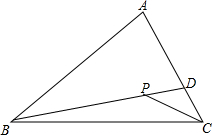 ŅŃÖŖŌŚČż½ĒŠĪABCÖŠ£¬“ęŌŚŅ»µćP£¬Į¬½ÓPB”¢PC£¬ŃÓ³¤BP½»ACÓŚµćD£¬ĒóÖ¤£ŗAB+AC£¾PB+PC£®
ŅŃÖŖŌŚČż½ĒŠĪABCÖŠ£¬“ęŌŚŅ»µćP£¬Į¬½ÓPB”¢PC£¬ŃÓ³¤BP½»ACÓŚµćD£¬ĒóÖ¤£ŗAB+AC£¾PB+PC£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ijŠ£ĪŖĮĖĮĖ½ā°ĖÄź¼¶Ń§ÉśµÄÉķĢå·¢ÓżĒéæö£¬“ÓČ«Ģå°ĖÄź¼¶µÄѧɜ֊³éČ”ĮĖŅ»Š©Ń§Éś½ųŠŠÉķøß²āĮ棬ĖłµĆŹż¾ŻČēĶ¼£¬ŌņøĆŠ£µÄ°ĖÄź¼¶Ń§ÉśµÄĘ½¾łÉķøßĪŖ162cm£®
ijŠ£ĪŖĮĖĮĖ½ā°ĖÄź¼¶Ń§ÉśµÄÉķĢå·¢ÓżĒéæö£¬“ÓČ«Ģå°ĖÄź¼¶µÄѧɜ֊³éČ”ĮĖŅ»Š©Ń§Éś½ųŠŠÉķøß²āĮ棬ĖłµĆŹż¾ŻČēĶ¼£¬ŌņøĆŠ£µÄ°ĖÄź¼¶Ń§ÉśµÄĘ½¾łÉķøßĪŖ162cm£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻC=90”ć£¬AMŹĒ”ĻBACµÄĘ½·ÖĻߣ¬CM=15cm£¬ÄĒĆ“µćMµ½ABµÄ¾ąĄėĪŖ15cm£®
ČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻC=90”ć£¬AMŹĒ”ĻBACµÄĘ½·ÖĻߣ¬CM=15cm£¬ÄĒĆ“µćMµ½ABµÄ¾ąĄėĪŖ15cm£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1øö | B£® | 2øö | C£® | 3øö | D£® | 4øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
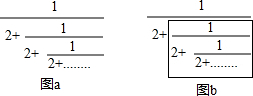 ¹Ū²ģĶ¼aĖłŹ¾ĖćŹ½£¬øĆĖćŹ½ÓÉĪŽŹż²ć·ÖŹżĻß¼°ĻąĶ¬µÄ¼ÓŹż2Ń»·Ē¶Ģ׶ų³É£¬ÓÉĶ¼bĪŅĆĒ·¢ĻÖ£¬ŅņĪŖÓŠĪŽŹż²ć·ÖŹżĻßĒ¶Ģ×£¬Ņņ“Ė·½æņÄŚµÄ²æ·ÖÓėÕūøöĖćŹ½ĻąĶ¬£¬ĪŅĆĒ¼ŁÉčĖćŹ½µÄ½į¹ūĪŖx£¬ÄĒĆ“¾ĶæÉŅŌ½«øĆĖćŹ½×Ŗ»Æ³É$\frac{1}{2+x}$£¬“Ó¶ųµĆµ½·½³Ģ$\frac{1}{2+x}$=x£®Ēó½ā³öøĆĖćŹ½µÄ½į¹ū
¹Ū²ģĶ¼aĖłŹ¾ĖćŹ½£¬øĆĖćŹ½ÓÉĪŽŹż²ć·ÖŹżĻß¼°ĻąĶ¬µÄ¼ÓŹż2Ń»·Ē¶Ģ׶ų³É£¬ÓÉĶ¼bĪŅĆĒ·¢ĻÖ£¬ŅņĪŖÓŠĪŽŹż²ć·ÖŹżĻßĒ¶Ģ×£¬Ņņ“Ė·½æņÄŚµÄ²æ·ÖÓėÕūøöĖćŹ½ĻąĶ¬£¬ĪŅĆĒ¼ŁÉčĖćŹ½µÄ½į¹ūĪŖx£¬ÄĒĆ“¾ĶæÉŅŌ½«øĆĖćŹ½×Ŗ»Æ³É$\frac{1}{2+x}$£¬“Ó¶ųµĆµ½·½³Ģ$\frac{1}{2+x}$=x£®Ēó½ā³öøĆĖćŹ½µÄ½į¹ū²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com