
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
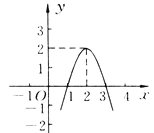
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
【答案】(1)x=1或x=3是方程ax2+bx+c=0的两个根;(2)l<x<3;(3)当x>2时,y随x的增大而减小;(4)k<2.
【解析】试题分析:(1)观察图形可以看出抛物线与x轴交于(1,0)和(3,0),即可解题
(2)根据抛物线y=ax2+bx+c,求得y>0的x取值范围即可解题;
(3)图中可以看出抛物线对称轴,即可解题;
(3)易求得抛物线解析式,根据方程△>0即可解题.
试题解析:(1)图中可以看出抛物线与x轴交于(1,0)和(3,0),
∴方程ax2+bx+c=0的两个根为x=1或x=3;
(2)不等式ax2+bx+c>0时,通过图中可以看出:当1<x<3时,y的值>0,
∴不等式ax2+bx+c>0的解集为(1,3);
(3)图中可以看出对称轴为x=2,
∴当x>2时,y随x的增大而减小;
(4)∵抛物线y=ax2+bx+c经过(1,0),(2,2),(3,0),
∴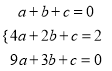 ,
,
解得:a=2,b=8,c=6,
∴2x2+8x6=k,移项得2x2+8x6k=0,
△=644(2)(6k)>0,
整理得:168k>0,
∴k<2时,方程ax2+bx+c=k有2个相等的实数根。


科目:初中数学 来源: 题型:
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
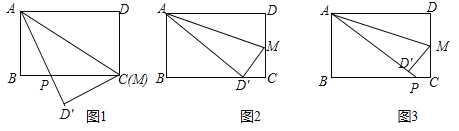
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
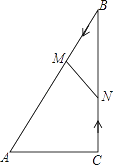
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发, 在
出发, 在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() 秒
秒![]() ,连接
,连接![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣2x﹣3>0.
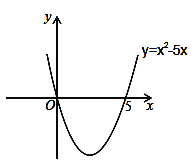
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为![]() ,这里“
,这里“![]() ”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为
”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为![]() (2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为
(2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为![]() n3.
n3.
通过对上以材料的阅读,请解答下列问题.
(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为_________________;
(2)计算![]() (n2-1)=________________.(填写最后的计算结果)
(n2-1)=________________.(填写最后的计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
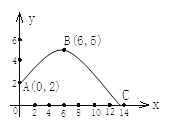
【题目】在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为B(6,5).
(1)求这个二次函数的表达式;
(2)该男生把铅球推出去多远?(精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
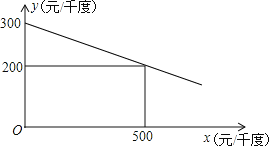
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )

A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com