
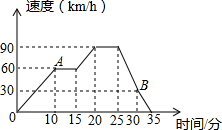
 如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:
如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题: 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
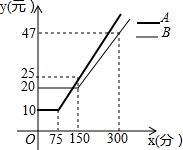 某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.
某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
| 桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
| 售价x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).
在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com