
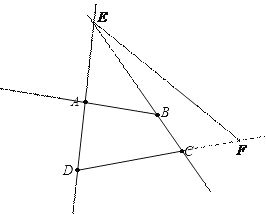
����Ŀ����������ͼ��ƽ�������ĸ���A��B��C��D��

��1������������仭ͼ:
�ٻ�����BA��
�ڻ�ֱ��AD��BC�ཻ�ڵ�E��
���ӳ��߶�DC�����߶�DC���ӳ�����ȡһ��F��ʹCF=BC��
������EF��
��2��ͼ����EΪ����Ľ��У�С��ƽ�ǵĽǹ��� ����
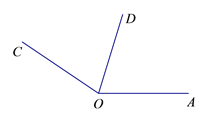
��������֪����AOC=146����ODΪ��AOC��ƽ���ߣ���AOB=90��������ͼ����ͼ��ʾ���벹ȫͼ�Σ������BOD�Ķ�����
���𰸡�����1��ͼ�μ�������2��8��II����1��17�㣨2��163��
�������������������������1������ֱ�ߡ����ߡ��߶ε��ص㻭��ͼ�μ��ɣ�
��2�����ݽǵĸ���й����˵�������������ɵ�ͼ�ν����������ǵĸ������ɣ�
��������OB���ڡ�AOC���ڲ�ʱ������ODƽ�֡�AOC�õ���AOD���������ɡ�BOD=��AOB-��AOD�������BOD��������������𰸣���OB���ڡ�AOC���ⲿʱ������ODƽ�֡�AOC�õ���AOD���������ɡ�BOD=��AOB+��AOD�������BOD���������������.
�����������������1����ͼ��
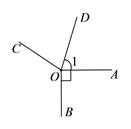
��2����EΪ����Ľ��У�С��ƽ�ǵĽ���8�����ʴ�Ϊ��8��
��II���� ODΪ��AOC��ƽ���ߣ���![]() ��
��
��![]() (��ƽ���ߵĶ���)��
(��ƽ���ߵĶ���)��
��1��������![]() ��
��![]() �ڲ�ʱ����ͼ��
�ڲ�ʱ����ͼ��

![]() ��
��
��2��������OB��![]() �ⲿʱ����ͼ��
�ⲿʱ����ͼ��
![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��C���߶�AD����CD��2AB��3��
��1������C���߶�AD���е�����BC��AB��ֵ��
��2����BC��![]() AD����BC��AB��ֵ��
AD����BC��AB��ֵ��
��3�����߶�AC����һ��P�������B�غϣ���AP��AC��DP����BP�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������������ε����ߣ������ֱ�������ε�һ�����ǣ� ��
A.![]() ��
�� ![]() ��
�� ![]()
![]()
B.2��3��4
C.3��4��5
D.6��8��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��2016����ҵ��ˮ��x���֣������Ӧ����ˮ��y��Ԫ��֮��ĺ�����ϵ��ͼ��
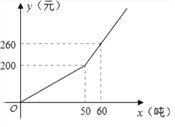
��1����x��50ʱ����y����x�ĺ�����ϵʽ��
��2����ij��ҵ2016��10�·ݵ�ˮ��Ϊ620Ԫ�������ҵ2016��10�·ݵ���ˮ����
��3��Ϊ������ҵ��Լ��ˮ��������2017��1�¿�ʼ������ˮ������80�ֵ���ҵ������ˮ�����ѣ��涨������ҵ����ˮ��x����80�֣������2016���շѱ���ȡˮ���⣬����80�ֵIJ���ÿ��������![]() Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
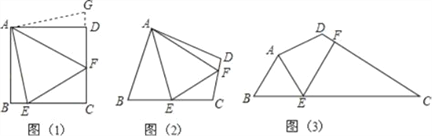
����Ŀ�����⣺��ͼ(1)����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬���ж�BE��EF��FD֮���������ϵ��
������֤����С�ϰѡ�ABE�Ƶ�A��ʱ����ת90������ADG,�Ӷ�����EF=BE+FD,��������ͼ��1��֤���������ۣ�
����������ͼ(2)���ı���ABCD��,��BAD��90��,AB=AD,��B+��D=180��,��E��F�ֱ��ڱ�BC��CD��,��EAF���BAD���� ��ϵʱ������EF=BE+FD��
��̽��Ӧ�á���ͼ(3)����ij����ͬһˮƽ���ϣ�����ͨ��Χ���ı���ABCD����֪AB=AD=80�ף���B=60�㣬��ADC=120�㣬��BAD=150�㣬��·BC��CD�Ϸֱ��о���E��F����AE��AD��DF=40��![]() ��1���ף���Ҫ��E��F֮����һ����ֱ��·����������·EF�ij������ȡ�������ο����ݣ�
��1���ף���Ҫ��E��F֮����һ����ֱ��·����������·EF�ij������ȡ�������ο����ݣ� ![]() =1.41��
=1.41�� ![]() =1.73��
=1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
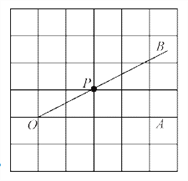
����Ŀ����ͼ����![]() �������������У���P��
�������������У���P��![]() �ı�OB�ϵ�һ����
�ı�OB�ϵ�һ����
��1������P��OB�Ĵ��ߣ���OA�ڵ�C������P��OA�Ĵ��ߣ�����ΪH��
��2���߶�PH�ij����ǵ�P��ֱ��__________�ľ�����
��3���߶�__________�ij����ǵ�C��ֱ��OB�ľ�����
��4���߶�PC��PH��OC�������߶δ�С��ϵ��__________������<������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����㣨��2����3������ƽ��3����λ����ƽ�ƺ�ĵ������Ϊ________
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com