
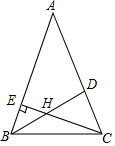
 在△ABC中,∠ABC=∠ACB=2∠A,BD是∠ABC的平分线,交AB边上的高CE于点H,求∠BHC的度数.
在△ABC中,∠ABC=∠ACB=2∠A,BD是∠ABC的平分线,交AB边上的高CE于点H,求∠BHC的度数.  口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
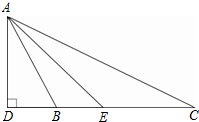 如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.
如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
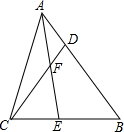 已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.
已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量学校教学楼的高度,王芳同学在她的脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到楼的顶部.如果王芳同学的身高是1.55m,她估计自己的眼睛距地面 AB=1.50m,同时量得 BE=30cm,BD=2.3m,这栋楼CD有多高?
如图,为了测量学校教学楼的高度,王芳同学在她的脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到楼的顶部.如果王芳同学的身高是1.55m,她估计自己的眼睛距地面 AB=1.50m,同时量得 BE=30cm,BD=2.3m,这栋楼CD有多高?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨但不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com