
【题目】折纸是一项有趣的活动,在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念. 今天,就让我们带着数学的眼光来玩一玩折纸.
实践操作
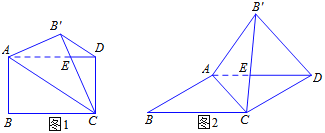
如图1,将矩形纸片ABCD沿对角线AC翻折,使点![]() 落在矩形ABCD所在平面内,
落在矩形ABCD所在平面内,![]() C和AD相交于点E,连接
C和AD相交于点E,连接![]() D.
D.
解决问题
(1)在图1中,①![]() D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
拓展应用
(3)在图2中,若∠B=30o,AB=![]() ,当A
,当A![]() ⊥AD时,BC的长度为_____.
⊥AD时,BC的长度为_____.
【答案】(1) BD′∥AC,菱形;(2)成立,理由见解析;(3)4或6或8或12.
【解析】
(1)①根据内错角相等两直线平行即可判断;
②根据菱形的判定方法即可解决问题;
(2)只要证明AE=EC,即可证明结论②成立;只要证明∠ADB′=∠DAC,即可推出B′D∥AC;
(3)先证得四边形ACB′D是等腰梯形,分四种情形分别讨论求解即可解决问题;
解:(1)①BD′∥AC.②将△AEC剪下后展开,得到的图形是菱形;
故答案为BD′∥AC,菱形;
(2)①选择②证明如下:
如图2,
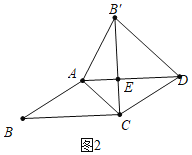
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵将△ABC沿AC翻折至△AB′C,
∴∠ACB′=∠ACB,
∴∠DAC=∠ACB′,
∴AE=CE,
∴△AEC是等腰三角形;
∴将△AEC剪下后展开,得到的图形四边相等,
∴将△AEC剪下后展开,得到的图形四边是菱形.
②选择①证明如下,
∵四边形ABCD是平行四边形,
∴AD=BC,
∵将△ABC沿AC翻折至△AB′C,
∵B′C=BC,
∴B′C=AD,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD
∴∠ADB′=∠DAC,
∴B′D∥AC.
(3)∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠B=30°,∴∠AB′C=∠CDA=30°,
∵△AB′D是直角三角形,
当∠B′AD=90°,AB>BC时,如图3中,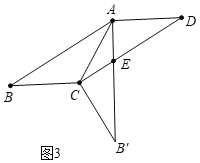
设∠ADB′=∠CB′D=y,
∴∠AB′D=y-30°,
解得y=60°,
∴∠AB′D=y-30°=30°,
∵AB′=AB=4![]()
![]()
∴BC=4,
当∠ADB′=90°,AB>BC时,如图4,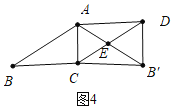
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠ADB′=90°,
∴四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵∠B=30°,AB=4![]()
![]()
当∠B′AD=90°,AB<BC时,如图5,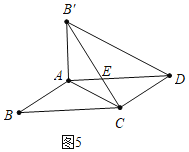
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
![]()
∴∠AB′C=30°,
∴AE=4,BE′=2AE=8,
∴AE=EC=4,
∴CB′=12,
当∠AB′D=90°时,如图6,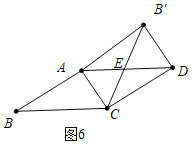
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是平行四边形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
![]()
![]()
∴已知当BC的长为4或6或8或12时,△AB′D是直角三角形.
故答案为:4或6或8或12;


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
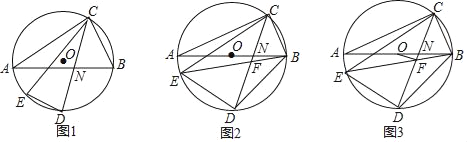
【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=![]() ,求线段OF的长.
,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.
(1)这50名学生每人一周内的零花钱数额的平均数是_______元/人;
(2)如果把全班50名学生每人一周内的零花钱按照不同数额人数绘制成扇形统计图,则一周内的零花钱数额为5元的人数所占的圆心角度数是_____度;
(3)一周内的零花钱数额为20元的有5人,其中有2名是女生, 3名是男生,现从这5人中选2名进行个别教育指导,请用画树状图或列表法求出刚好选中2名是一男一女的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,面积为150.
,面积为150.

(1)尺规作图:作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;(不要求写作法,保留作图痕迹)
;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求出点![]() 到两条直角边的距离.
到两条直角边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
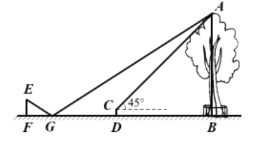
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
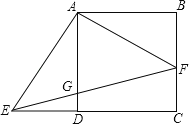
【题目】如图,在正方形ABCD中,F是边BC上一点(点F与点B、点C均不重合),AE⊥AF,AE交CD的延长线于点E,连接EF交AD于点G.
(1)求证:BFFC=DGEC;
(2)设正方形ABCD的边长为1,是否存在这样的点F,使得AF=FG.若存在,求出这时BF的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
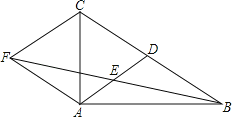
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列网格由小正方形组成,点![]() 都在正方形网格的格点上.
都在正方形网格的格点上.
(1)在图1中画出一个以线段![]() 为边,且与
为边,且与![]() 面积相等但不全等的格点三角形;
面积相等但不全等的格点三角形;
(2)在图2和图3中分别画出一个以线段![]() 为边,且与
为边,且与![]() 相似(但不全等)的格点三角形,并写出所画三角形与
相似(但不全等)的格点三角形,并写出所画三角形与![]() 的相似比.(相同的相似比算一种)
的相似比.(相同的相似比算一种)
(1)
(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com