
【题目】如图所示,有一个只允许单向通过的窄道口,通常情况下,每分钟可以通过9人.一天王老师到达道口时,发现由于拥挤,每分钟只能有3人通过道口,此时,自己前面还有36人等待通过(假定先到达的先过,王老师过道口的时间忽略不计),通过道口后,还需7分钟到达学校.

(1)此时,若绕道而行,要15分钟才能到达学校,从节省时间考虑,王老师应选择绕道去学校,还是选择通过拥挤的道口去学校?
(2)若在王老师等人的维持下,几分钟后秩序恢复正常(维持秩序期间,每分钟仍有3人通过道口),结果王老师比在拥挤的情况下提前6分钟通过道口,问维持秩序的时间是多长?
科目:初中数学 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
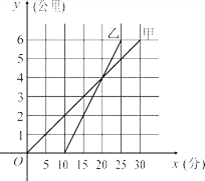
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y= ![]() x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.
x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.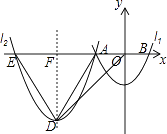
(1)求抛物线l2的解析式;
(2)求证:△ADE∽△DOE;
(3)半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F(﹣6,0),运动速度为1单位/秒,运动时间为t秒,⊙P绕着点C顺时针旋转90°得⊙P1 , 随着⊙P的运动,求P1的运动路径长以及当⊙P1与y轴相切的时候t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com