
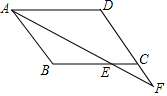
 如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.  应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
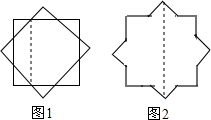 如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.
如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲班 | B. | 乙班 | C. | 丙班 | D. | 丁班 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
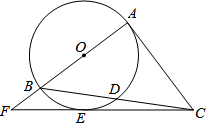 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
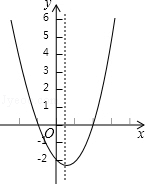 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com