
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| x-1 |
| x+1 |
| x2 |
| x-1 |
| 3 |
| x+1 |
| 2x |
| x2+1 |
| x-1 |
| x+1 |
| (x+1)-2 |
| x+1 |
| 2 |
| x+1 |
| x2 |
| x-1 |
| x2-1+1 |
| x-1 |
| (x+1)(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
| x-1 |
| x+2 |
| 2x-1 |
| x+1 |
| x-1 |
| x+2 |
| (x+2)-3 |
| x+2 |
| 3 |
| x+2 |
| 2x-1 |
| x+1 |
| 2(x+1)-3 |
| x+1 |
| 3 |
| x+1 |
| 2x-1 |
| x+1 |
| 3 |
| x+1 |



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| x-1 |
| x+1 |
| x2 |
| x-1 |
| 3 |
| x+1 |
| 2x |
| x2+1 |
| x-1 |
| x+1 |
| (x+1)-2 |
| x+1 |
| 2 |
| x+1 |
| x2 |
| x-1 |
| x2-1+1 |
| x-1 |
| (x+1)(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
| x-1 |
| x+2 |
| 2x-1 |
| x+1 |
| 2x2-1 |
| x+1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 =
=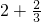 =
=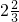 £®ŌŚ·ÖŹ½ÖŠ£¬¶ŌÓŚÖ»ŗ¬ÓŠŅ»øö×ÖÄøµÄ·ÖŹ½£¬µ±·Ö×ӵēĪŹż“óÓŚ»ņµČÓŚ·ÖÄøµÄ“ĪŹżŹ±£¬ĪŅĆĒ³ĘÖ®ĪŖ”°¼Ł·ÖŹ½”±£»µ±·Ö×ӵēĪŹżŠ”ÓŚ·ÖÄøµÄ“ĪŹżŹ±£¬ĪŅĆĒ³ĘÖ®ĪŖ”°Õę·ÖŹ½”±£®ĄżČē£ŗ
£®ŌŚ·ÖŹ½ÖŠ£¬¶ŌÓŚÖ»ŗ¬ÓŠŅ»øö×ÖÄøµÄ·ÖŹ½£¬µ±·Ö×ӵēĪŹż“óÓŚ»ņµČÓŚ·ÖÄøµÄ“ĪŹżŹ±£¬ĪŅĆĒ³ĘÖ®ĪŖ”°¼Ł·ÖŹ½”±£»µ±·Ö×ӵēĪŹżŠ”ÓŚ·ÖÄøµÄ“ĪŹżŹ±£¬ĪŅĆĒ³ĘÖ®ĪŖ”°Õę·ÖŹ½”±£®ĄżČē£ŗ £¬
£¬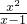 ÕāŃłµÄ·ÖŹ½¾ĶŹĒ¼Ł·ÖŹ½£»
ÕāŃłµÄ·ÖŹ½¾ĶŹĒ¼Ł·ÖŹ½£»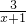 £¬
£¬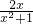 ÕāŃłµÄ·ÖŹ½¾ĶŹĒÕę·ÖŹ½£®ĄąĖĘµÄ£¬¼Ł·ÖŹ½Ņ²æÉŅŌ»ÆĪŖ“ų·ÖŹ½£Ø¼“£ŗÕūŹ½ÓėÕę·ÖŹ½ŗĶµÄŠĪŹ½£©£®
ÕāŃłµÄ·ÖŹ½¾ĶŹĒÕę·ÖŹ½£®ĄąĖĘµÄ£¬¼Ł·ÖŹ½Ņ²æÉŅŌ»ÆĪŖ“ų·ÖŹ½£Ø¼“£ŗÕūŹ½ÓėÕę·ÖŹ½ŗĶµÄŠĪŹ½£©£®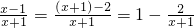 £»
£» 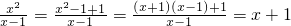 +
+ £®
£®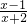 »ÆĪŖ“ų·ÖŹ½£»
»ÆĪŖ“ų·ÖŹ½£»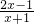 µÄÖµĪŖÕūŹż£¬ĒóxµÄÕūŹżÖµ£»
µÄÖµĪŖÕūŹż£¬ĒóxµÄÕūŹżÖµ£»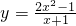 Ķ¼ĻóÉĻĖłÓŠŗįׯ×ų±ź¾łĪŖÕūŹżµÄµćµÄ×ų±ź£®
Ķ¼ĻóÉĻĖłÓŠŗįׯ×ų±ź¾łĪŖÕūŹżµÄµćµÄ×ų±ź£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| x-1 |
| x+1 |
| x2 |
| x-1 |
| 3 |
| x+1 |
| 2x |
| x2+1 |
| x-1 |
| x+1 |
| (x+1)-2 |
| x+1 |
| 2 |
| x+1 |
| x2 |
| x-1 |
| x2-1+1 |
| x-1 |
| (x+1)(x-1)+1 |
| x-1 |
| 1 |
| x-1 |
| x-1 |
| x+2 |
| 2x-1 |
| x+1 |
| 2x2-1 |
| x+1 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com