
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.

【答案】(1)证明见解析;(2)等腰直角三角形.
【解析】试题分析:
(1)先证四边形ABDF是平行四边形,再证结论;
(2)由四边形ADCF是正方形来证明△ABC是等腰直角三角形.
试题解析:
(1)证明:∵点D、E分别是边BC、AC的中点,∴DE∥AB,
∵AF∥BC,∴四边形ABDF是平行四边形,∴AF=BD,则AF=DC=AD,
∵AF∥BC,∴四边形ADCF是平行四边形;
(2)当△ABC是等腰直角三角形时,四边形ADCF是正方形,
理由:∵四边形ADCF是正方形,∴∠ADC=90°,AC=DF,AF=DC.
∵点D,E分别是边BC,AC的中点,AB=2DE,∴AB=DF,所以AB=AC.
∴四边形ABDF是平行四边形,∴AF=BD,∴BD=CD=AD,
∴∠BAC=90°,
∴△ABC是等腰直角三角形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A按逆时针方向旋转120°得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接BB',若AC'∥BB',则∠C'AB'的度数为( )
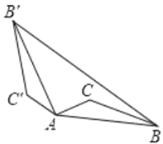
A.20°B.30°C.40°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
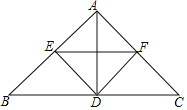
【题目】如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() <0等.那么如何求出它们的解集呢?
<0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则![]() >0;若a<0,b<0,则
>0;若a<0,b<0,则![]() >0;
>0;
(2)若a>0,b<0,则![]() <0;若a<0,b>0,则
<0;若a<0,b>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则 或 .
<0,则 或 .
根据上述规律,求不等式![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
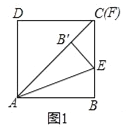
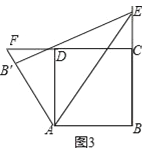
【题目】如图,四边形ABCD是正方形,点E在直线BC上,连接AE.将△ABE沿AE所在直线折叠,点B的对应点是点B′,连接AB′并延长交直线DC于点F.
(1)当点F与点C重合时如图1,证明:DF+BE=AF;
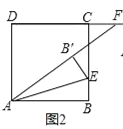
(2)当点F在DC的延长线上时如图2,当点F在CD的延长线上时如图3,线段DF、BE、AF有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com