如果一次函数y=kx+b的自变量x取值范围是-3≤x≤2,相应的函数值的范围是-8≤y≤5,求此函数解析式.
分析:根据一次函数的增减性,可知本题分两种情况:①当k>0时,y随x的增大而增大,把x=-3,y=-8;x=2,y=5代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式;②当k<0时,y随x的增大而减小,把x=-3,y=5;x=2,y=-8代入一次函数的解析式y=kx+b,运用待定系数法即可求出函数的解析式.
解答:解:根据题意,①当k>0时,y随x增大而增大,
∴当x=-3,y=-8;x=2,y=5,
∴
,
解得:
,
∴函数解析式为y=
x-
;
②当k<0时,函数值随x增大而减小,
∴当x=2时,y=-8,x=-3时,y=5,
∴
,
解得
,
∴函数解析式为y=-
x-
.
因此,函数解析式为y=
x-
或y=-
x-
.
点评:本题主要考查一次函数的性质,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小,注意要分情况讨论.



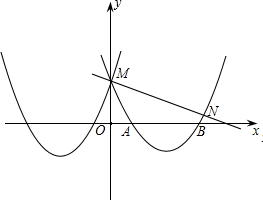 点M,与x轴交于点A和B.
点M,与x轴交于点A和B.