
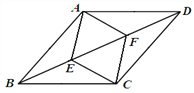
【题目】如图,点E、F为菱形ABCD对角线BD的三等分点.
(1)试判断四边形AECF的形状,并加以证明;
(2)若菱形ABCD的周长为52,BD为24,试求四边形AECF的面积.
【答案】(1)菱形;(2) 40
【解析】试题分析:(1)根据菱形的对角线互相垂直平分可得AC⊥BD,AO=OC,EO=OF,再求出BO=OD,然后根据对角线互相垂直平分的四边形是菱形证明;
(2)根据菱形的四条边都相等求出边长AB,根据菱形的对角线互相平分求出OB,然后利用勾股定理列式求出AO,再求出AC,最后根据菱形的面积等于对角线乘积的一半列式计算即可得解.
试题解析:
(1)四边形ABCD为菱形.
理由如下:如图,连接AC交BD于点O,
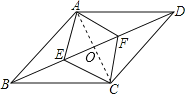
∵四边形AECF是菱形,
∴AC⊥BD,AO=OC,EO=OF,
又∵点E、F为线段BD的两个三等分点,
∴BE=FD,
∴BO=OD,
∵AO=OC,
∴四边形ABCD为平行四边形,
∵AC⊥BD,
∴四边形ABCD为菱形;
(2)∵四边形ABCD为菱形,且周长为52,
∴AB=13,
∵BD=24,E、F为菱形ABCD对角线BD的三等分点,
∴OB=![]() BD=
BD=![]() ×24=12,EF=
×24=12,EF=![]() ,
,
由勾股定理得,AO=![]() ,
,
∴AC=2AO=2×5=10,
∴S四边形AECF=![]() EFAC=
EFAC=![]() ×8×10=40.
×8×10=40.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)求证:AD+BE=DE;
(3)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
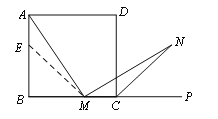
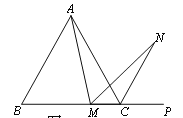
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程2y2﹣7=3y的二次项系数、一次项系数、常数项分别是( )
A.2,﹣3,﹣7B.﹣2,﹣3,﹣7C.2,﹣7,3D.﹣2,﹣3,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形,是因式分解的为( )
A.6ab=2a·3b B.(x+5)(x-2)=x2+3x-10
C.x2-8x+16=(x-4)2 D.x2-9+6x=(x-3)(x+3)+6x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com