
【题目】如图,已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连接EF,M为EF的中点.

(1)请判断四边形PECF的形状,并说明理由;
(2)随着P点在AB上位置的改变,CM的长度是否也会改变?若不变,求CM的长度;若有变化,求CM的变化范围.
【答案】(1)矩形;(2)![]()
【解析】
(1)首先根据勾股定理的逆定理判断三角形ABC是直角三角形,然后根据三个角都是直角的四边形是矩形即可得解;
(2)CM的长度会改变.连接PC,证得四边形PECF是矩形,得到EF=PC,求出PC的范围,即可得到得到EF的范围,即可得到CM 的范围.
(1)在△ABC中,AC=3,BC=4,AB=5.
∵AC2+BC2=32+42=52=AB2,∴∠ACB=90°.
∵PE⊥AC,PF⊥BC,∴∠PEC=∠ACB=∠CFP=90°,∴四边形PECF是矩形;
(2)CM的长度会改变,理由是:
连接PC,由(1)证得四边形PECF是矩形,∴EF=PC.
过点C作CD⊥AB,此时CD=PC且PC最小,∴PC![]() 2.4.
2.4.
∵点P是斜边AB上 (不与A、B重合),∴PC<BC=4,∴PC的范围是2.4≤PC<4,即EF的范围是2.4≤EF<4.
∵M为EF的中点,∴CM![]() EF,∴CM的范围是
EF,∴CM的范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
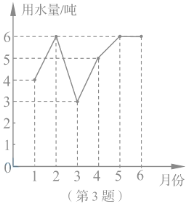
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
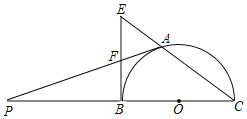
【题目】如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.
(1)求证:BF=EF;
(2)若AF=![]() ,半⊙O的半径为2,求PA的长度.
,半⊙O的半径为2,求PA的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.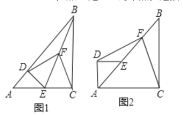
(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.
(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.
(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=﹣![]() (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=
(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=![]() (k>0,x>0)于点P,且OAMP=12,
(k>0,x>0)于点P,且OAMP=12,
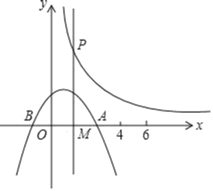
(1)求k值;
(2)当t=1时,求AB的长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x![]() ,且满足4x
,且满足4x![]() 6,通过L位置随t变化的过程,直接写出t的取值范围。
6,通过L位置随t变化的过程,直接写出t的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,以A为圆心,AB长为半径作弧BE,CD于E,若AB=4,则阴影部分的面积为_____(结果保留π和根号).
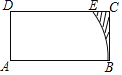
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB⊥AC,过点D作DE⊥AD交直线AC于点E,点O是对角线AC的中点,点F是线段AD上一点,连接FO并延长交BC于点G.
(1)如图1,若AC=4,cos∠CAD=![]() ,求△ADE的面积;
,求△ADE的面积;
(2)如图2,点H为DC是延长线上一点,连接HF,若∠H=30°,DE=BG,求证:DH=CE+![]() FH.
FH.
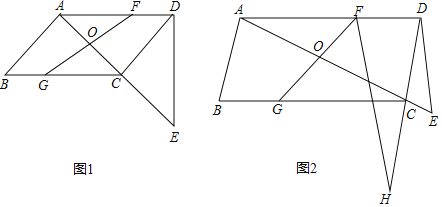
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
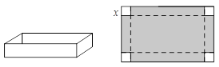
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有人说:“数学是思维的体操”,运用和掌握必要的“数学思想”和“数学方法”是取胜数学的重要法宝.阅读下列例题:
(1)解方程:x2﹣2|x|﹣3=0.
解:①当x≥0时,有x2﹣2x﹣3=0,解得x1=﹣1(舍去),x2=3.
②当x<0时,有x2+2x﹣3=0,解得x1=1(舍去),x2=﹣3.所以,原方程的解是x=3或﹣3.(数学的分类讨论思想)试解方程:x2﹣|x﹣1|﹣1=0.
(2)设a3+a﹣1=0,求a3+a+2018的值.
解:由a3+a﹣1=0得a3+a=1,代入,有a3+a+2018=1+2018=2019(整体代入或换元思想)
试一试:当a是一元二次方程x2﹣2018x+1=0的一个根时,求:a2﹣2017a+![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com