
分析 由mx+n>0的解集为x>$\frac{2}{5}$得$\frac{n}{m}$=-$\frac{2}{5}$,且m>0、n<0,从而得出nx-m<0的解集是x>$\frac{m}{n}$,即x>-$\frac{5}{2}$.
解答 解:∵mx+n>0,即x>-$\frac{n}{m}$的解集为x>$\frac{2}{5}$,
∴-$\frac{n}{m}$=$\frac{2}{5}$,即$\frac{n}{m}$=-$\frac{2}{5}$,且m>0,
∴n<0,
则nx-m<0的解集是x>$\frac{m}{n}$,即x>-$\frac{5}{2}$,
故答案为x>-$\frac{5}{2}$.
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
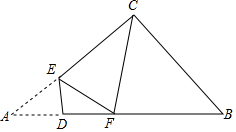 如图,在Rt△ABC中,AC=8,BC=6,点D为斜边AB上一点,DE⊥AB交AC于点E,将△AED沿DE翻折,点A的对应点为点F.如果△EFC是直角三角形,那么AD的长为$\frac{7}{5}$或5.
如图,在Rt△ABC中,AC=8,BC=6,点D为斜边AB上一点,DE⊥AB交AC于点E,将△AED沿DE翻折,点A的对应点为点F.如果△EFC是直角三角形,那么AD的长为$\frac{7}{5}$或5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.
小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
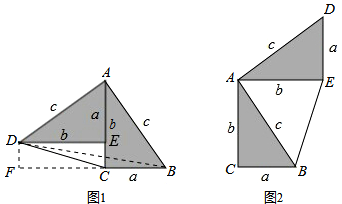 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com