
【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.

(1)如图①,在AB上取一点D,将纸片沿OD翻折,使点A落在BC边上的点E处,求D、E两点的坐标;
(2)如图②,若OE上有一动点P(不与O,E重合),从点O出发,以每秒1个单位的速度沿OE方向向点E匀速运动,设运动时间为t秒(0<t<5),过点P作PM⊥OE交OD于点M,连接ME,求当t为何值时,以点P、M、E为顶点的三角形与△ODA相似?
【答案】(1)点D的坐标为(5,2.5);(2)当t=2.5或4时,以点P、M、E为顶点的三角形与△ODA相似.
【解析】
(1)由翻折的性质可知OE=5,然后利用勾股定理可求得CE=3,从而求得点E的坐标,然后在三角形EDB中,利用翻折的性质和勾股定理可求得AD的长,从而可求得点D的坐标;
(2)首先证明∠EPM=90°,首先根据相似三角形的性质可知∠PEM=∠DOA或∠PME=∠DOA,然后利用相似三角形的性质可求得t的值.
(1)由翻折的性质可知:OE=OA=5,
在Rt△OCE中,CE=![]() =3,
=3,
∴点E的坐标为(3,4),
∴EB=CB﹣CE=5﹣3=2,
设AD=x,则BD=4﹣x,
由翻折的性质可知:ED=AD=x,
在Rt△BED中,EB2+BD2=ED2,即22+(4﹣x)2=x2,
解得:x=2.5,
∴AD=2.5,
∴点D的坐标为(5,2.5);
(2)由翻折的性质可知:∠OED=∠DAO=90°,∠DOE=∠DOA,
∵PM∥ED,
∴∠MPE+∠PED=180°,
∴∠MPE=90°,
∴∠MPE=∠DAO,
当点P、M、E为顶点的三角形与△ODA相似时,有△PEM∽△AOD或△PME∽△AOD,
∴∠PEM=∠DOA或∠PME=∠DOA,
①当∠PEM=∠DOA时,在△OPM和△EPM中,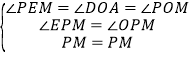 ,
,
∴△OPM≌△EPM,
∴PE=PO.
∴t=2.5;
②当∠PME=∠DOA时,OP=t,则PE=5﹣t.
∵∠DOE=∠DOA,
∴tan∠DOE=tan∠DOA,
∴![]() ,
,
∴PM=![]() ,
,
∵∠PME=∠DOA,
∴tan∠PME=tan∠DOA,
∴![]() ,即
,即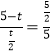 ,
,
解得:t=4,
综上所述,当t=2.5或4时,以点P、M、E为顶点的三角形与△ODA相似.


科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2x2﹣8x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为( )
A. 8 B. ﹣10 C. ﹣42 D. ﹣24
查看答案和解析>>
科目:初中数学 来源: 题型:
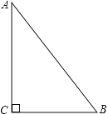
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm,若动点P从点C开始,沿C→A→B→C的路径运动一周,且速度为每秒2cm,设运动时间为t秒,当t=_____时,点P与△ABC的某两个顶点构成等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FOED=ODEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“感冒”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后y与x成反比例如图。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
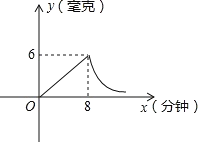
(1)药物燃烧时,y关于x的函数关系式为___,自变量x的取值范围是___;药物燃烧后y关于x的函数关系式为___.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过___分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病毒,那么此次消毒有效吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
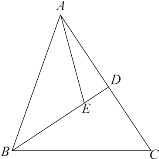
【题目】如图,△ABC中,AE=BE,∠AED =∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB = CB,∠AED =4∠EAD,求∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com