
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
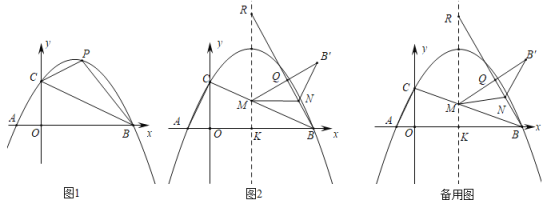
(1)点P为线段BC上方抛物线上(不与B、C重合)的一动点,连接PC、PB,当△PBC面积最大时,在y轴找点D,使得PD﹣![]() OD的值最小时,求这个最小值.
OD的值最小时,求这个最小值.
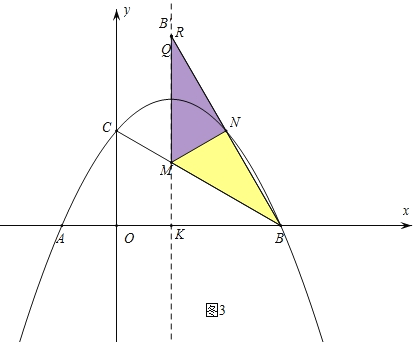
(2)如图2,抛物线对称轴与x轴交于点K,与线段BC交于点M,在对称轴上取一点R,使得KR=12(点R在第一象限),连接BR.已知点N为线段BR上一动点,连接MN,将△BMN沿MN翻折到△B'MN.当△B'MN与△BMR重叠部分(如图中的△MNQ)为直角三角形时,直接写出此时点B'的坐标.
【答案】(1)PD﹣![]() OD的值最小
OD的值最小![]() ;(2)B'(2
;(2)B'(2![]() ,12)或B'(
,12)或B'(![]() ,4)时,△MNQ为直角三角形.
,4)时,△MNQ为直角三角形.
【解析】
(1)由已知可求![]() ,
,![]() ,
,![]() ,求出直线BC的解析式,进而设点P的坐标,再根据
,求出直线BC的解析式,进而设点P的坐标,再根据![]() 面积最大时确定P点的坐标,最后根据最短路径的知识求出
面积最大时确定P点的坐标,最后根据最短路径的知识求出![]() 的最小值;
的最小值;
(2)根据题意,重叠部分可以分两种情况进行讨论,即①当MN⊥B'M,②当MN⊥BR时,![]() 为直角三角形,进而求出B'的坐标即可.
为直角三角形,进而求出B'的坐标即可.
(1)由已知可求![]() ,
,![]() ,
,![]() ,
,
∴直线BC的解析式为![]() ,直线AC的解析式为
,直线AC的解析式为![]() ,
,
设点![]() ,
,
∵过点P与直线BC垂直的直线解析式为![]() ,
,
∴设直线![]() 与直线
与直线![]() 的交点Q的坐标为
的交点Q的坐标为
![]() ,
,
∴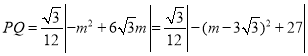 ,
,
当m=![]() 时,PQ有最大,此时
时,PQ有最大,此时![]() 面积最大,
面积最大,
∴![]() ,
,
如下图,作P点关于y轴的对称点![]() ,作直线
,作直线![]() ,
,
过点P'作直线![]() 的垂线交y轴于点D,交直线
的垂线交y轴于点D,交直线![]() 于点M,
于点M,
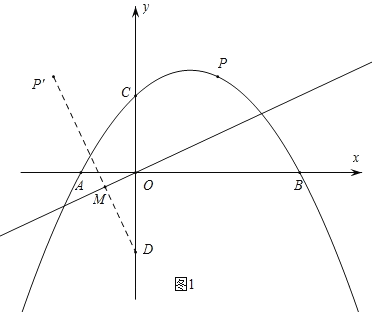
∵PD=P'D,∠DOM=60°,
∴MD=![]() OD,
OD,
∴![]() ,
,
∴![]() OD的最小值为P'M;
OD的最小值为P'M;
∵P'D的解析式为y=![]() ,
,
∴![]() ,
,
∴P'M=![]() ,
,
∴![]() 的值最小
的值最小![]() ;
;
(2)①当MN⊥B'M时,![]() 为直角三角形,
为直角三角形,
对称轴![]() ,
,
∴![]() ,
,![]() ,
,
∴KB=![]() ,
,
直线BC的解析式为![]() ,
,
∴![]() ,
,
∴MK=4,MB=8,
∴RM=8,
∴MR=KB,
∵![]() ,
,
∴∠KRB=30°,
∴∠B'=30°,
∴QM=4,B'Q=![]() ,
,
∴RQ=4,
∴QN=![]() ,
,
∴![]() ;
;
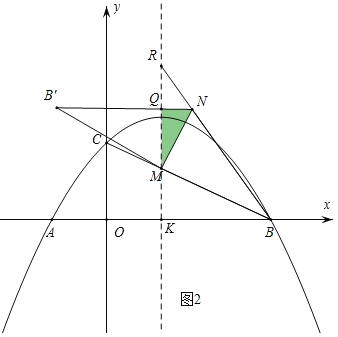
②当MN⊥BR时,![]() 为直角三角形,
为直角三角形,
∵∠MBN=∠MB'N=30°,∠KRB=30°,
∴B'与R重合,
∴![]() ;
;
综上所述:![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.


科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:
①若![]() ,则
,则![]() ;
;
②当![]() 时,若
时,若![]() ,则
,则![]() ;
;
③直角三角形中斜边上的中线等于斜边的一半;
④矩形的两条对角线相等.
其中原命题与逆命题均为真命题的个数是( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的东北方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处.
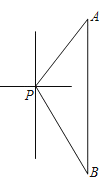
(1)若灯塔P周围50海里范围内有暗礁,海轮从A处到B处的途中,是否有触礁危险?
(2)若海轮以每小时30海里的速度从A处到B处,试判断海轮能否在5小时内到达B处,并说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新的教学改革的推动下,某中学初年级积极推进英语小班教学.为了了解一段时间以来的英语小班教学的学习效果,年级组织了多次定时测试,现随机选取甲,乙两个班,从中各抽取20名同学在某一次定时测试中的英语成绩,过程如下,请补充完整
收集数据:
甲班的20名同学的英语成绩统计(单位:分)
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计(满分为100分)(单位:分)
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
数量分数/ 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据:
请回答下列问题:
(1)完成下表:
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a= |
乙班 | 80.35 | b= | 78 |
甲班成绩得分扇形图(x表示分数)
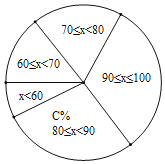
(2)在班成绩行分的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数 ,c= .
(3)根据以上数据,你认为 班(填“甲”或“乙”)的同学的学习效果更好一些,你的理由是: ;
(4)若英语定时成绩不低于80分为优秀,请估计全年级1600人中优秀人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,线段![]() 是⊙
是⊙![]() 的直径,过
的直径,过![]() 点作直线
点作直线![]() 交⊙
交⊙![]() 于
于![]() 、
、![]() 两点,过
两点,过![]() 点作
点作![]() 的角平分线交⊙
的角平分线交⊙![]() 于
于![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]()
(1)证明![]() 是⊙
是⊙![]() 的切线
的切线
(2)证明![]()
(3)若⊙![]() 的直径为10,
的直径为10,![]() ,求
,求![]()
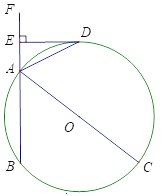
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴和
轴和![]() 轴建立如图所示的平面直角坐标系,
轴建立如图所示的平面直角坐标系,![]() 是
是![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() 重合),过
重合),过![]() 点的反比例函数
点的反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
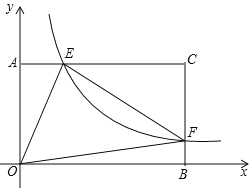
(1)若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)当点![]() 在
在![]() 上移动时,
上移动时,![]() 与
与![]() 的面积差记为
的面积差记为![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
(3)是否存在这样的点![]() ,使得
,使得![]() 为直角三角形?若存在,求出此时点
为直角三角形?若存在,求出此时点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
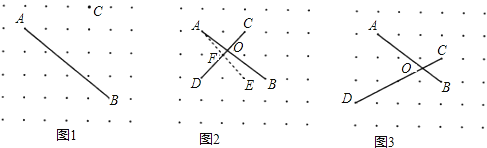
小明观察一个由1×1正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出交点与垂足之间的数值.
请回答:
(1)如图1,A、B、C是点阵中的三个点,请在点阵中找到点D,作出线段CD,使得CD⊥AB;
(2)如图2,线段AB与CD交于点O,小明在点阵中找到了点E,连接AE.恰好满足AE⊥CD于E,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
请你帮小明计算:OC= OF= ;
参考小明思考问题的方法,解决问题:
(3)如图3,线段AB与CD交于点O.在点阵中找到点E,连接AE,满足AE⊥CD于F.计算: OC= ,OF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
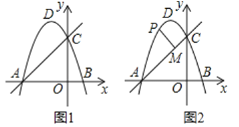
【题目】如图1,抛物线y=﹣x2+bx+c经过点A,B,C,已知点A和C的坐标分别是(﹣4,0)和(0,4),点P在抛物线y=﹣x2+bx+c上.
(1)求抛物线的解析式及顶点D的坐标;
(2)如图2,当点P在线段AC的上方,点P的横坐标记为t,过点P作PM⊥AC于点M,当PM=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点E是抛物线对称轴上与点D不重合的一点,F是平面内的一点,当四边形CPEF是正方形时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com