
 如图,矩形ABCD的对角线交于O点,延长CB至点E,使CE=AC,点F是AE的中点,连结BF、DF,且DF与AC交于P点.
如图,矩形ABCD的对角线交于O点,延长CB至点E,使CE=AC,点F是AE的中点,连结BF、DF,且DF与AC交于P点.分析 (1)BF⊥DF,理由是:作辅助线,构建全等三角形,证明BF=FM,在等腰三角形BDM中,根据三线合一的性质得出结论;
(2)设∠FDB=x,则∠FBD=∠E=∠M=5x,在△MBD中根据三角形的内角和列方程求出x的值,得出△DOC是等边三角形;
(3)先证明△APQ是等边三角形得AP=AQ,设CD=x,则AC=2x,AD=$\sqrt{3}$x,根据同角的三角函数列比例式$\frac{BE}{AB}=\frac{AQ}{AD}$,表示出AQ,再利用直角三角形斜边中线等于斜边一半表示出AF的长,最后计算比值即可.
解答  解:(1)BF⊥DF,理由是:
解:(1)BF⊥DF,理由是:
∵四边形ABCD为矩形,
∴MD∥BC,
∴∠M=∠EBF,∠MAF=∠AEB,
∵AF=EF,
∴△AFM∽△EFB,
∴AM=BE,BF=FM,
∵AD=BC,
∴AD+AM=BC+BE,
即DM=CE,
∵CE=AC,AC=BD,
∴BD=DM,
∵BF=FM,
∴BF⊥DF;
(2)在Rt△ABE中,
∵F是AE的中点,
∴BF=$\frac{1}{2}$AE=AF=EF,
∴AF=FE=BF=FM,
∴∠AMF=∠FAM=∠E=∠FBD,
设∠FDB=x,则∠FBD=∠E=∠M=5x,
在△MBD中得:5x+5x+2x=180,
∴x=15,
∴∠ADB=2x=30°,
∴∠ODC=60°,
∵OD=OC,
∴△OCD是等边三角形;
(3)∵△OCD是等边三角形;
∴∠CPD=∠PDC=∠PCD=60°,
∴∠APQ=60°,
∵AB∥CD,
∴∠QAP=∠PCD=60°,
∴△APQ是等边三角形,
∴AP=AQ,
设CD=x,则AC=2x,AD=$\sqrt{3}$x,
∴BE=EC-BC=2x-$\sqrt{3}$x,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{x}^{2}+(2x-\sqrt{3}x)^{2}}$=($\sqrt{6}-\sqrt{2}$)x,
∴AF=$\frac{1}{2}$AE=$\frac{(\sqrt{6}-\sqrt{2})x}{2}$,
∵AC=EC,
∴∠E=∠EAC=$\frac{180-30}{2}$=75°,
∴∠EAB=15°,
∴tan∠EAB=tan∠QDA,
∴$\frac{BE}{AB}=\frac{AQ}{AD}$,
∴$\frac{2x-\sqrt{3}x}{x}=\frac{AQ}{\sqrt{3}x}$,
∴AQ=(2$\sqrt{3}$-3)x
∴$\frac{AP}{AF}$=$\frac{AQ}{AF}$=$\frac{(2\sqrt{3}-3)x}{\frac{(\sqrt{6}-\sqrt{2})x}{2}}$=$\frac{3\sqrt{2}-\sqrt{6}}{2}$.
点评 本题是四边形的综合题,考查了矩形的性质、全等三角形的性质和判定、等腰三角形的三线合一的性质及直角三角形斜边中线的性质,综合性较强,但难度不大;尤其是等腰三角形角度的变化较多,要认真书写;在几何证明中,如果求两条线段的比值时,而已知中没有任何一边的长度时,可以设一边为x,将其它各边分别用x的式子表示,也可以相应求出比值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2002 | B. | 2003 | C. | 2004 | D. | 2005 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
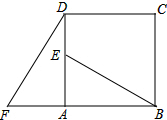 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.
如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com