
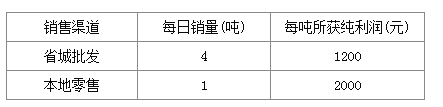
【题目】种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
【答案】(1)y=-800x+44000;(2)用4天时间运往省城批发,6天在本地零售,可以使张华所获纯利润最大,最大利润为31200元.
【解析】试题分析:(1)根据题意可以得到y与x的函数关系式;
(2)根据题意可以得到关于x的不等式,从而可以求得x的取值范围,再结合(1)中的函数关系式,本题得以解决.
试题解析:(1)由题意可得,
y=1200x+2000(22x)=800x+44000,
即销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式是y=800x+44000;
(2)∵草莓必须在10天内售出(含10天),
∴![]() +22x10,
+22x10,
解得,x16,
∵y=800x+44000,800<0,
∴在函数y=800x+44000中,y随x的增大而减小,
∴当x=16时,y取得最大值,此时y=800×16+44000=31200,
2216=4,104=6,
即用4天时间运往省城批发,6天在本地零售,可以使张华所获纯利润最大,最大利润为31200元.


科目:初中数学 来源: 题型:
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
【答案】(1)0,1,2;(2)证明见解析;(3)![]()
【解析】试题分析:(1)根据0次幂的意义和乘方的意义进行计算即可;
(2)观察各等式得到2的相邻两个非负整数幂的差等于其中较小的2的非负整数幂,即2n-2n-1=2n-1(n为正整数);
(3)由于21-20=20,22-21=21,23-22=22,…22018-22017=22017,然后把等式左边与左边相加,右边与右边相加即可求解.
试题解析:(1)21-20=1=20;22-21=2=21;23-22=4=22,
故答案为:0,1,2;
(2)观察可得:2n-2n-1=2n-1(n为正整数),证明如下:
2n-2n-1=2×2n-1-2n-1=2n-1×(2-1)=2n-1;
(3)∵21-20=20,
22-21=21,
23-22=22,
…
22018-22017=22017,
∴22018-20=20+21+22+23+…+22016+22017,
∴20+21+22+23+…+22016+22017的值为22018-1.
【题型】解答题
【结束】
27
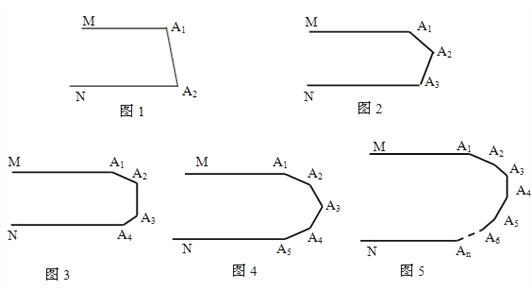
【题目】(1) 如图1,MA1∥NA2,则∠A1+∠A2=_________度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=_________ 度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=_________度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=_________度.
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=_________ 度.
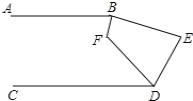
(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°,求∠BFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, ![]() ,
, ![]()
(1)用尺规作图作AB边上中垂线DE,交AC于点D,交AB于点E。(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知l1//l2,射线MN分别和直线l1,l2交于点A,B,射线ME分别和直线l1,l2交于点C,D,点P在射线MN上运动(P点与A,B,M三点不重合),设∠PDB=α ,∠PCA=β ,∠CPD=γ .
(1)如果点P在A,B两点之间运动时,α,β,γ之间有何数量关系?请说明理由;
(2)如果点P在A,B两点之外运动时,α,β,γ之间有何数量关系?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com