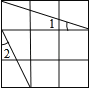
【题目】如图，在3×3的正方形网格中标出了∠1和∠2．则∠1+∠2= ．
【答案】45°
【解析】
试题分析：根据图形，先将角进行转化，再根据勾股定理的逆定理，求得∠ACB=90°，由等腰三角形的性质，推得∠1+∠2=45°．
解：连接AC，BC．
根据勾股定理，AC=BC=
，AB=
．
∵（）2+（）2=（）2，
∴∠ACB=90°，∠CAB=45°．
∵AD∥CF，AD=CF，
∴四边形ADFC是平行四边形，
∴AC∥DF，
∴∠2=∠DAC（两直线平行，同位角相等），
在Rt△ABD中，
∠1+∠DAB=90°（直角三角形中的两个锐角互余）；
又∵∠DAB=∠DAC+∠CAB，
∴∠1+∠CAB+∠DAC=90°，
∴∠1+∠DAC=45°，
∴∠1+∠2=∠1+∠DAC=45°．
故答案为：45°．
科目：初中数学 来源： 题型：
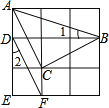
【题目】已知，如图在△ABC中，∠B＞∠C，AD是BC边上的高，AE平分∠BAC．
（1）若∠B=40°，∠C=30°，则∠DAE= ；
（2）若∠B=80°，∠C=40°，则∠DAE= ；
（3）由（1）、（2）我能猜想出∠DAE与∠B、∠C之间的关系为 ．理由如下：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数
和一次函数y=2x﹣1，其中一次函数的图象经过（a，b），（a+2，b+k）两点．
（1）求：反比例函数的解析式．
（2）如图，已知点A在第一象限，且同时在上述两函数的图象上．求点A的坐标．
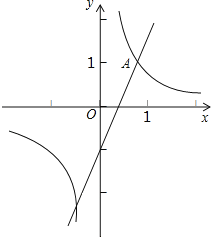
（3）利用（2）的结果，问在x轴上是否存在点P，使得△AOP为等腰三角形？若存在，把符合条件的P点坐标直接写出来；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，点B和点C分别为∠MAN两边上的点，AB=AC．
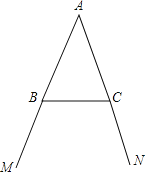
（1）按下列语句画出图形：
①AD⊥BC，垂足为D；
②∠BCN的平分线CE与AD的延长线交于点E；
③连接BE．
（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形： ≌ ， ≌ ；并选择其中的一对全等三角形，予以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．
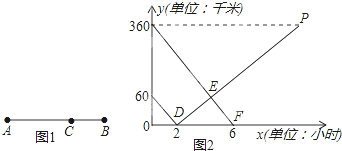
（1）填空：A，B两地相距 千米；货车的速度是 千米/时．
（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数表达式；
（3）客、货两车何时相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】菱形ABCD一条对角线长为6，边AB长为方程y2﹣7y+10=0的一个根，则菱形ABCD周长为（ ）
A． 8 B． 20 C． 8或20 D． 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com