
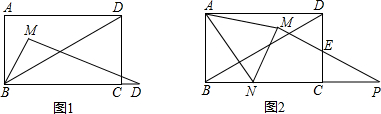
���� ��1����ͼ1�У�����M��MH��BC����ֱΪH����MK��BC����BD�ڵ�T����CD��K����T��TG��BC��ֱΪG�����ı���MHGT�Ǿ��Σ����MT�ij���Ȼ��������M�˶���BD���õ�ʱ�䣮
��2���������������ۣ��ٵ�0��t��1.4ʱ���ڵ�1.4��t��2.2ʱ���۵�2.2��t��4ʱ�ֱ��г���������ʽ��
��3���������ۣ��ٵ�AN=NMʱ���ڵ�AM=MNʱ���۵�AN=AMʱ�����ݹ��ɶ����з��̼��ɣ�
��� �⣺��1����ͼ1�У�����M��MH��BC����ֱΪH����MK��BC����BD�ڵ�T����CD��K����T��TG��BC��ֱΪG�����ı���MHGT�Ǿ��Σ�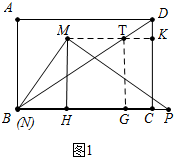
���ı���ABCD�Ǿ��Σ�
���A=90�㣬��AB=6��AD=8��
��BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10��
����ת֪��MNP=��ABD��MN=AB=6��NP=BD=10��
�֡ߡ�MNP+��NMH=90�㣬��ABD+��DNP=90�㣬
���NMH=��DNP��sin��DNC=$\frac{DC}{DN}$=$\frac{3}{5}$=sin��NMH=$\frac{NH}{BM}$��
��NH=3.6��cos��DNC=cos��NMH=$\frac{NC}{BD}=\frac{MH}{NM}=\frac{8}{10}$��
��MH=4.8=TG��
��tan��DNC=$\frac{DC}{BC}$=$\frac{6}{8}$=$\frac{TG}{NG}$��
��NG=6.4��CG=TK=1.6��
��HG=NG-NH=6.4-3.6=2.8=MT��
��t=MT��2=2.8��2=1.4��
��2������ͼ2�У���0��t��1.4ʱ���ص����ֵ�������������TNCGK�������TH��BC��H��KR��CD��R��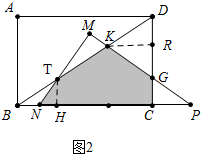
��BN=CP=2t��TH=CG=$\frac{3}{2}$t��DG=6-$\frac{3}{2}$t��KR=4-t��
��y=S��BDC-S��BNT-S��KDG=24-$\frac{1}{2}$•2t•$\frac{3}{2}$t-$\frac{1}{2}$•��6-$\frac{3}{2}$t��•��4-t��=-$\frac{9}{4}$t2+6t+12��
����ͼ3�У���1.4��t��2.2ʱ���ص����ֵ���������ı���MNCR�����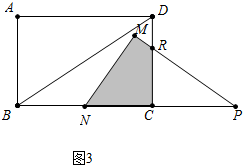
y=S��MNR-S��PRC=24-$\frac{1}{2}$•2t•$\frac{3}{2}$t=-$\frac{3}{4}$t2+24��
����ͼ4�У���2.2��t��4ʱ���ص����ֵ�������ǡ�RNC�����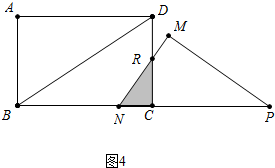
y=$\frac{1}{2}$•��8-2t��•$\frac{4}{3}$��8-2t��=$\frac{8}{3}$t2-$\frac{64}{3}$t+$\frac{128}{3}$��
��������y=$\left\{\begin{array}{l}{-\frac{9}{4}{t}^{2}+6t+12}&{��0��t��1.4��}\\{-\frac{3}{4}{t}^{2}+24}&{��1.4��t��2.2��}\\{\frac{8}{3}{t}^{2}-\frac{64}{3}t+\frac{128}{3}}&{��2.2��t��4��}\end{array}\right.$��
��3����3������ͼ5�У���AN=NMʱ��x=0�룻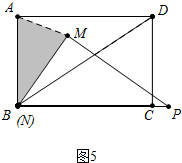
����ͼ6�У�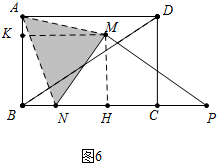
��AM=MNʱ��MK=BH=BN+NH=2x+$\frac{18}{5}$��MH=BK=$\frac{24}{5}$��
��AK2+MK2=36��
�ࣨ6-$\frac{24}{5}$��2+��2x+$\frac{18}{5}$��2=36��
��ã�x=$\frac{6\sqrt{6}-9}{5}$�룬��x=$\frac{-6\sqrt{6}-9}{5}$��ȥ����
����ͼ6����AN=AMʱ��MK=BH=BN+NH=2x+$\frac{18}{5}$��MH=KB=$\frac{24}{5}$��
��AB2+BN2=AK2+MK2
��36+4x2=��6-$\frac{24}{5}$��2+��2x+$\frac{18}{5}$��2
��ã�x=$\frac{3}{2}$�룮
����������ʹ�á�AMN��Ϊ���������ε�x��ֵ�У�0���$\frac{3}{2}$���$\frac{6\sqrt{6}-9}{5}$�룮
���� ������Ҫ������ͼ�ε�ƽ�Ʊ任����ת�任�����ε����ʡ����������ε����ʵ�֪ʶ������Ĺؼ��Ƿ�����������ȷ����ͼ�Σ�ѧ��ָ�����������ѧ���÷��̵�˼�������⣬ע�⿼������Ҫȫ�棬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
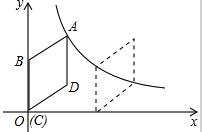 ��ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���C��ԭ��O�غϣ���B��y����������ϣ���A�ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�����ABCD����ƽ��ʹ��D��4��3�����ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�������ABCDƽ�Ƶľ���Ϊ$\frac{20}{3}$��
��ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���C��ԭ��O�غϣ���B��y����������ϣ���A�ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�����ABCD����ƽ��ʹ��D��4��3�����ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ�������ABCDƽ�Ƶľ���Ϊ$\frac{20}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
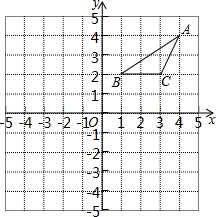 ��ͼ����ABC���������ֱ���A��4��4����B��1��2����C��3��2�����ֽ���ABC��ԭ��O��ʱ�뷽����ת90��õ���A��B��C�䣬�ٽ���A��B��C������ƽ��4����λ���ȵõ���A��B��C�壬�����е��������ȷ���ǣ�������
��ͼ����ABC���������ֱ���A��4��4����B��1��2����C��3��2�����ֽ���ABC��ԭ��O��ʱ�뷽����ת90��õ���A��B��C�䣬�ٽ���A��B��C������ƽ��4����λ���ȵõ���A��B��C�壬�����е��������ȷ���ǣ�������| A�� | A�䣨4��-4�� | B�� | B�䣨-1��2�� | C�� | A�壨-4��-4�� | D�� | C�壨-2��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�߶�AB=4��OΪAB���е㣬P��ƽ���ڵ�-�����㣬���˶������б���OP=1���䣬����BP����PB�Ƶ�P��ʱ����ת90�㵽PC������BC��AC�����߶�AC����ȡֵ��Χ��$\sqrt{2}$��AC��3$\sqrt{2}$��
��ͼ����֪�߶�AB=4��OΪAB���е㣬P��ƽ���ڵ�-�����㣬���˶������б���OP=1���䣬����BP����PB�Ƶ�P��ʱ����ת90�㵽PC������BC��AC�����߶�AC����ȡֵ��Χ��$\sqrt{2}$��AC��3$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y+1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y+1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y-1}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
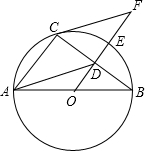 ��ͼ��ABΪԲO��ֱ������C��E��Բ�ϣ��ҵ�E�ǻ�BC���е㣬OE����BC�ڵ�D����F��OE���ӳ����ϣ��ҡ�BCF=��BAC��BC=8��DE=2��
��ͼ��ABΪԲO��ֱ������C��E��Բ�ϣ��ҵ�E�ǻ�BC���е㣬OE����BC�ڵ�D����F��OE���ӳ����ϣ��ҡ�BCF=��BAC��BC=8��DE=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
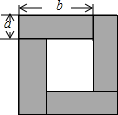 ��ͼ����4��ȫ�ȵij�����ƴ��һ�������Ρ������Σ�
��ͼ����4��ȫ�ȵij�����ƴ��һ�������Ρ������Σ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com