
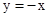 ;②
;②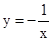 ;③
;③ ;④
;④ 中,y随x的增大而减小的函数有( )
中,y随x的增大而减小的函数有( )| A.1个 | B.2个 | C.3个 | D.4个 |
 的性质,当
的性质,当 时, y的值随x的值增大而增大;当
时, y的值随x的值增大而增大;当 时,函数y的值随x的值增大而减小. 因此,函数
时,函数y的值随x的值增大而减小. 因此,函数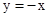 是y随x的增大而减小的函数.
是y随x的增大而减小的函数. 的性质,当
的性质,当 时函数图象的每一支上,y随x的增大而减小;当
时函数图象的每一支上,y随x的增大而减小;当 时,函数图象的每一支上,y随x的增大而增大. 因此,函数
时,函数图象的每一支上,y随x的增大而增大. 因此,函数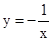 和
和 都不是y随x的增大而减小的函数.
都不是y随x的增大而减小的函数. 的性质,当
的性质,当 时,在对称轴左边y随x的增大而减小,在对称轴右边y随x的增大而增大;当
时,在对称轴左边y随x的增大而减小,在对称轴右边y随x的增大而增大;当 时,在对称轴左边y随x的增大而增大,在对称轴右边y随x的增大而减小.因此,因为
时,在对称轴左边y随x的增大而增大,在对称轴右边y随x的增大而减小.因此,因为 ,所以当
,所以当 时y随x的增大而减小,当
时y随x的增大而减小,当 时y随x的增大而增大,因此函数
时y随x的增大而增大,因此函数 不是y随x的增大而减小的函数.
不是y随x的增大而减小的函数.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| x | ﹣7 | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 |
| y | ﹣27 | ﹣13 | ﹣3 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 两种产品,根据市场调研,发现如下信息:
两种产品,根据市场调研,发现如下信息: 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在二次函数关系
(吨)之间存在二次函数关系 .当
.当 时,
时, ;当
;当 时,
时, .
. 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在正比例函数关系
(吨)之间存在正比例函数关系 .
. 两种产品共10吨,请设计一个营销方案,使销售
两种产品共10吨,请设计一个营销方案,使销售 两种产品获得的利润之和最大,最大利润是多少?
两种产品获得的利润之和最大,最大利润是多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
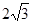 ,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.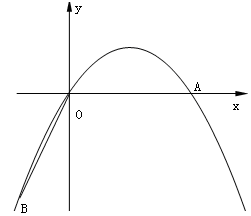
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| x | … | 0 | 1 | 3 | 4 | … |
| y | … | 2 | 4 | 2 | -2 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com