
【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.
的图象与性质.
因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … |
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 |
|
| 1 |
|
| … |
| … |
|
| 2 | 3 | 5 |
|
| 0 |
|
| … |
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示).
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③![]() 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
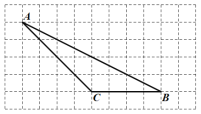
【题目】如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB∥CD,E在直线AB上,且EF⊥EG,EF交直线CD于点M.EG交直线CD于点N.

(1)若∠1=34°,求∠2的度数;(2)若∠2=2∠1,直接写出图中等于4∠1的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→)(0,1)→(0,2)→……,且每秒移动一个单位,那么第2018秒时,点所在位置的坐标是( ).

A. (6,44)B. (38,44)C. (44,38)D. (44,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县近两个多月持续高温而且没有降雨导致居民用水严重紧缺,为了加强市民的节水意识,我县制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨2元,超过10吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤10,请写出y与x的函数关系式.
(2)若x>10,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费29元,那么这个月该户用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、字相乘法等等,将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫做分组分解.
例如:![]()
利用这种分组的思想方法解决下列问题:
(1)分解因式![]() ;
;
(2)![]() 三边a,b,c满足
三边a,b,c满足![]() 判断
判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com