
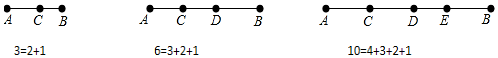
Ζ÷Έω Θ®1Θ©ΗυΨί“―÷Σ’“Ιφ¬…Θ§ΖΔœ÷ΘΚ1ΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2=3ΧθΘ§2ΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2+3=6ΧθΘ§
¥”ΕχΒΟ≥ω6ΗωΒψ ±Θ§œΏΕΈΒΡΧθ ΐΘΜ
Θ®2Θ©ΗυΨίΘ®1Θ©÷–ΒΡΫα¬έΒΟ≥ωnΗωΒψ ±œΏΕΈΒΡΧθ ΐΘΜ
Θ®3Θ©¥”ΥΡ±Ώ–ΈΓΔΈε±Ώ–ΈΒ»“ά¥ΈΒΟ≥ωΙφ¬…Θ§¥”n±Ώ–Έ1ΗωΕΞΒψ≥ωΖΔΩ…“‘ΫΪ’βΗωn±Ώ–ΈΖ÷≥…n-2Ηω»ΐΫ«–ΈΘ§¥”ΕχΝ– ΫΈΣΘΚn-2=2016Θ§ΦΤΥψ≥ωnΒΡ÷ΒΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΘ®1Θ©œΏΕΈAB…œ”–1ΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2=3ΧθΘ§
œΏΕΈAB…œ”–2ΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2+3=6ΧθΘ§
œΏΕΈAB…œ”–3ΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2+3+4=10ΧθΘ§
œΏΕΈAB…œ”–6ΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2+Γ≠+6+7=$\frac{7ΓΝΘ®7+1Θ©}{2}$=28ΧθΘΜ
Ι ¥πΑΗΈΣΘΚ28ΘΜ
Θ®2Θ©”…Θ®1Θ©ΒΟΘΚœΏΕΈAB…œ”–nΗωΒψ ±Θ§œΏΕΈΉήΙ≤”–ΘΚ1+2+3+Γ≠+n+n+1=$\frac{Θ®n+1Θ©Θ®1+n+1Θ©}{2}$=$\frac{Θ®n+1Θ©Θ®n+2Θ©}{2}$ΧθΘΜ
Ι ¥πΑΗΈΣΘΚ$\frac{Θ®n+1Θ©Θ®n+2Θ©}{2}$ΘΜ
Θ®3Θ©¥”ΥΡ±Ώ–ΈΒΡ“ΜΗωΕΞΒψ≥ωΖΔΘ§Ζ÷±πΝ§Ϋ”’βΗωΕΞΒψ”κΤδ”ύΗςΕΞΒψΘ§Ω…ΫΪ’βΗωΕύ±Ώ–ΈΖ÷Ην≥…2Ηω»ΐΫ«–ΈΘ§
¥”Έε±Ώ–ΈΒΡ“ΜΗωΕΞΒψ≥ωΖΔΘ§Ζ÷±πΝ§Ϋ”’βΗωΕΞΒψ”κΤδ”ύΗςΕΞΒψΘ§Ω…ΫΪ’βΗωΕύ±Ώ–ΈΖ÷Ην≥…3Ηω»ΐΫ«–ΈΘ§
Γ≠
¥”n±Ώ–ΈΒΡ“ΜΗωΕΞΒψ≥ωΖΔΘ§Ζ÷±πΝ§Ϋ”’βΗωΕΞΒψ”κΤδ”ύΗςΕΞΒψΘ§Ω…ΫΪ’βΗωΕύ±Ώ–ΈΖ÷Ην≥…2016Ηω»ΐΫ«–ΈΘ§
‘ρn-2=2016Θ§
n=2018Θ§
¥πΘΚ¥ΥΕύ±Ώ–ΈΒΡ±Ώ ΐΈΣ2018Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΆΦ–ΈάύΒΡΙφ¬…ΧβΦΑΕύ±Ώ–ΈΕ‘Ϋ«œΏΈ ΧβΘ§Ά®ΙΐΖ÷Έω’“ΒΫ±δΜ·Ιφ¬…Κσ÷±Ϋ”άϊ”ΟΙφ¬…«σΫβΘ°


 AΦ”ΫπΧβ œΒΝ–¥πΑΗ
AΦ”ΫπΧβ œΒΝ–¥πΑΗ »Ϊ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
»Ϊ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° |  | BΘ° |  | CΘ° |  | DΘ° |  |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
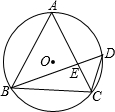 »γΆΦΘ§“―÷ΣΓςABCΡΎΫ””ΎΓ―OΘ§D «Γ―O…œ“ΜΒψΘ§Ν§ΫαBDΓΔCDΘ§ACΓΔBDΫΜ”ΎΒψEΘ°
»γΆΦΘ§“―÷ΣΓςABCΡΎΫ””ΎΓ―OΘ§D «Γ―O…œ“ΜΒψΘ§Ν§ΫαBDΓΔCDΘ§ACΓΔBDΫΜ”ΎΒψEΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | BΘ° | 2+$\sqrt{2}$=2$\sqrt{2}$ | CΘ° | $\sqrt{12}$-$\sqrt{10}$=$\sqrt{2}$ | DΘ° | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com