
【题目】A、B两厂在公路的同侧,现欲在公路边建一货场C.
(1)若要使货场到两厂的距离相等,请在图1中作出此时货场的位置.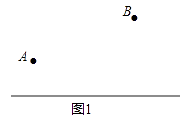
(2)若要求所修公路(即A、B两厂到货场的距离之和)最短,请在图2中作出货场的位置.(用尺规作图,保留作图痕迹,不必写作法)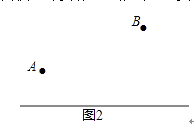
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: 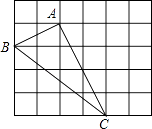
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 , CD的长为 , AD的长为;
(3)△ACD为三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积? 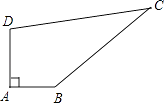
查看答案和解析>>
科目:初中数学 来源: 题型:
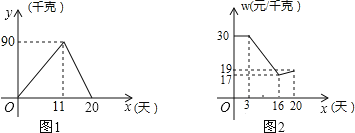
【题目】小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的价格w(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.
(1)观察图象,直接写出当0≤x≤11时,日销售量y与上市时间x之间的函数解析式为 ;
当11≤x≤20时,日销售量y与上市时间x之间的函数解析式为 .
(2)试求出第11天的销售金额;
(3)若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
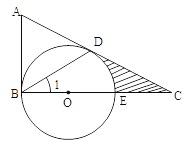
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com