
【题目】如图所示,![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,B,E,C在一条直线上
,B,E,C在一条直线上![]() 下列结论:
下列结论:![]() 是
是![]() 的平分线;
的平分线;![]() ;
;![]() ;
;![]() 线段DE是
线段DE是![]() 的中线;
的中线;![]() 其中正确的有 ()个.
其中正确的有 ()个.

A.2B.3C.4D.5
【答案】A
【解析】
根据全等三角形的对应角相等得出∠ABD=∠EBD,即可判断①;先由全等三角形的对应边相等得出BD=CD,BE=CE,再根据等腰三角形三线合一的性质得出DE⊥BC,则∠BED=90°,再根据全等三角形的对应角相等得出∠A=∠BED=90°,即可判断②;根据全等三角形的对应角相等得出∠ABD=∠EBD,∠EBD=∠C,从而可判断∠C,即可判断③;根据全等三角形的对应边相等得出BE=CE,再根据三角形中线的定义即可判断④;根据全等三角形的对应边相等得出BD=CD,但A、D、C可能不在同一直线上,所以AD+CD可能不等于AC.
解:①∵△ADB≌△EDB,
∴∠ABD=∠EBD,
∴BD是∠ABE的平分线,故①正确;
②∵△BDE≌△CDE,
∴BD=CD,BE=CE,
∴DE⊥BC,
∴∠BED=90°,
∵△ADB≌△EDB,
∴∠A=∠BED=90°,
∴AB⊥AD,
∵A、D、C可能不在同一直线上
∴AB可能不垂直于AC,故②不正确;
③∵△ADB≌△EDB,△BDE≌△CDE,
∴∠ABD=∠EBD,∠EBD=∠C,
∵∠A=90°
若A、D、C不在同一直线上,则∠ABD+∠EBD+∠C≠90°,
∴∠C≠30°,故③不正确;
④∵△BDE≌△CDE,
∴BE=CE,
∴线段DE是△BDC的中线,故④正确;
⑤∵△BDE≌△CDE,
∴BD=CD,
若A、D、C不在同一直线上,则AD+CD>AC,
∴AD+BD>AC,故⑤不正确.
故选:A.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】现有四张质地均匀,大小完全相同的卡片,在其正面分别标有数字﹣1,﹣2,2,3,把卡片背面朝上洗匀,从中随机抽出一张后,不放回,再从中随机抽出一张,则两次抽出的卡片所标数字之和为正数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
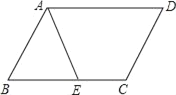
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E.
(1)在AD上求作点F,使点F到CD和BC的距离相等;
(要求:尺规作图,保留作图痕迹,不写作法)
(2)判断四边形AECF是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
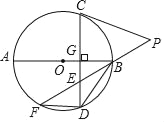
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连结CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)求证:CD=BF;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12 米,BC=24 米,动点P从点A始沿边AB向B以2 米/秒的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4 米/秒的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x 秒,四边形APQC的面积为y 米2.
(1)求y与x之间的函数关系式并写出自变量x的取值范围;
(2)四边形APQC的面积能否等于172米2.若能,求出运动的时间;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com