
分析 第1斜列的数字的个数是1,第2斜列的数字的个数是2,第3斜列的数字的个数是3,第4斜列的数字的个数是4,…,第n斜列的数字的个数是n,根据等差数列的求和公式,求出前61斜列的数字的个数是多少;然后根据奇数斜列从左下角到右上角,数字逐渐增加;偶数斜列从左下角到右上角,数字逐渐减小,判断出1893排在第几行,第几列即可.
解答 解:如图: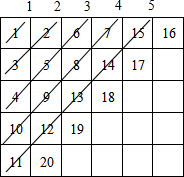
∵(1+2+3+…+61)
=(1+61)×61÷2
=62×61÷2
=1891,
∴前61斜列的数字个数是1891个,
∴1893在第62斜列,
∵偶数斜列从左下角到右上角,数字逐渐减小,
∴1893在第62斜列,从右上角开始的第二个数,
∴1893排在第2行,第61列.
点评 (1)此题主要考查了探寻数字规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:①第n斜列的数字的个数是n;②奇数斜列从左下角到右上角,数字逐渐增加;③偶数斜列从左下角到右上角,数字逐渐减小.
(2)此题还考查了等差数列的求和方法,要熟练掌握.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com