练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在棋盘中建立如图所示的直角坐标系，三颗棋子A，O，B的位置如图,它们的坐标分别是(-1,1),(0,0)和(1,0).

    （1）如图2，添加棋子C，使A，O，B，   C四颗棋子成为一个轴对称图形，请在图  中画出该图形的对称轴.

    （2）在其他格点位置添加一颗棋子P，使A,O,B,P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置的坐标.（写出2个即可）


    （1）如图.                              

    （2）(-1,-1),  (0,-1),  (2,1)

     



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    知ABC ，内角A、B、C所对边长分别为a、b、c，满足：=

    .

    （1）求角C的大小.

    （2）若，C=，求a、b的值（a>b）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    孔明同学在距某电视塔塔底水平距离500米处，看塔顶的仰角为20°（不考虑身高因素），则此塔高约为　　米（结果保留整数，参考数据：sin20°≈0.3420，sin70°≈0.9397，tan20°≈0.3640，tan70°≈2.7475）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    把代数式分解因式，结果正确的是（)

    A．  B．    C．    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小亮对60名同学进行节水方法选择的问卷调查（每人选择一项），人数统计如图，如果绘制成扇形统计图，那么表示“一水多用”的扇形圆心角的度数是    .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


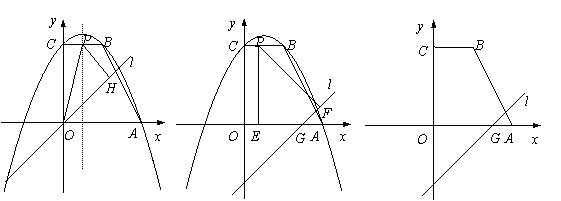
    如图，直角梯形ABCO的两边OA,OC在坐标轴的正半轴上，BC∥x轴，OA=OC=4，以直线x=1为对称轴的抛物线过A,B,C三点.

    （1）求该抛物线的函数解析式.

    （2）已知直线l的解析式为y=x+m，它与x轴交于点G，在梯形ABCO的一边上取点P.

    ①当m=0时，如图1，点P是抛物线对称轴与BC的交点，过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积.

    ②当m=-3时，过点P分别作x轴、直线l的垂线，垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在，求出点P的坐标；若不存在，请说明理由.

     


    （图1）             图2 ）                 （备用图）

                        备用图
     
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


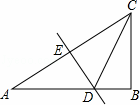
    如图，在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E两点．若BD=2，则AC的长是（　　）

    　

    A．

    4

    B．

    4

    C．

    8

    D．

    8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


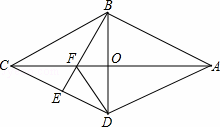
    如图，在四边形ABCD中，AB=AD，CB=CD，AC与BD相交于O点，OC=OA，若E是CD上任意一点，连接BE交AC于点F，连接DF．

    （1）证明：△CBF≌△CDF；

    （2）若AC=2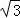，BD=2，求四边形ABCD的周长；

    （3）请你添加一个条件，使得∠EFD=∠BAD，并予以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：x（x+3）﹣（x+1）2，其中x=+1．

    查看答案和解析>>

    同步练习册答案