
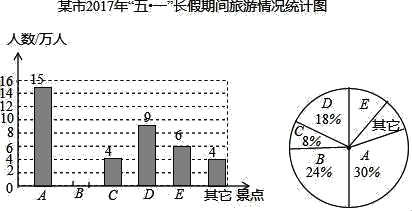
【题目】随着道路交通的不断完善,某市旅游业快速发展,该市旅游景区有A、B、C、D、E等著名景点,市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图(不完整)如下所示,根据相关信息解答下列问题:
(1)2017年“五一”期间,该市旅游景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)在等可能性的情况下,甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少?请用画树状图或列表加以说明.
【答案】(1)50、108°;(2)![]()
【解析】
(1)利用![]() ,即可以求出总人数,然后利用A占总人数的30%,根据360°×30%这个式子,可以求出景点A所占扇形图的度数.
,即可以求出总人数,然后利用A占总人数的30%,根据360°×30%这个式子,可以求出景点A所占扇形图的度数.
(2)作出树状图,得到所有可能的情况,即可以求出甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少.
(1)该市旅游景点共接待游客15÷30%=50(万人),
扇形统计图中A景点所对应的圆心角的度数是360°×30%=108°,
B景点的人数为50×24%=12(万人),
补全条形图如下:
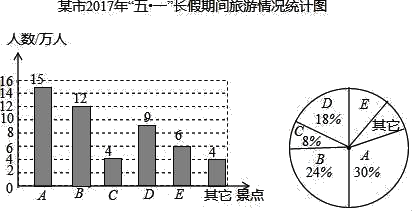
故答案为: 50、108°;
(2)画树状图可得:
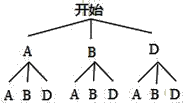
∵共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种,
∴同时选择去同一个景点的概率=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(2,4).

(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:
①在图中找一点P,使得P到AB、AC的距离相等,且PA=PB;
②在x轴上找一点Q,使得△QAB的周长最小,并求出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验中学为了解学生“最适合自己的考前减压方式”,在九年级范围内开展了一次抽样调查,学生必须在四类选项中选择一项,小明根据调查结果绘制了如下尚不完整的统计图.
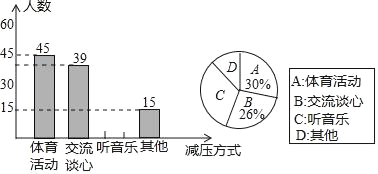
请根据以上信息解答下列问题:
(1)这次抽样调查中,抽查的学生人数为______人.
(2)请补全条形统计图.
(3)扇形统计图中“其他”所对应扇形圆心角为______度.
(4)若实验中学九年级有700人,请估计采用“听音乐”作为减压方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
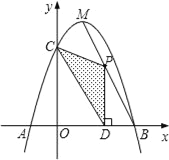
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG,AE,FG 分别交射线CD 于点 PH,连结 AH,若 P 是 CH 的中点,则△APH 的周长为( )
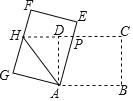
A. 15 B. 18 C. 20 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
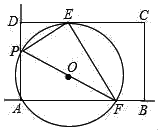
【题目】如图,矩形ABCD中,AD=10,CD=15,E是边CD上一点,且DE=5,P是射线AD上一动点,过A,P,E三点的⊙O交直线AB于点F,连结PE,EF,PF,设AP=m.
(1)当m=6时,求AF的长.
(2)在点P的整个运动过程中.
①tan∠PFE的值是否改变?若不变,求出它的值;若改变,求出它的变化范围.
②当矩形ABCD恰好有2个顶点落在⊙O上时,求m的值.
(3)若点A,H关于点O成中心对称,连结EH,CH.当△CEH是等腰三角形时,求出所有符合条件的m的值.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (1)阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ= QR = RS,(这个条件很重要哦!)勾 尺的一边 MN 满足M, N, Q三点共线(所以PQ ⊥ MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE //BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP:
请完成第三步操作,图中∠ABC的三等分线是射线 、 .
(2)在(1)的条件下补全三等分∠ABC的主要证明过程:
∵ ,BQ ⊥ PR,
∴BP= BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)
∴∠RBQ=∠PBQ,
∵PT⊥BC,PQ⊥BQ,PT=PQ,
∴∠ = ∠ . (角的内部到角的两边距离相等的点在角的平分线上)
∴∠ = = ∠ = ∠
(3)在(1)的条件下探究:
∠ABS=![]() ∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC外部画出∠ABV =
∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC外部画出∠ABV =![]() ∠ABC(无需写画法,保留画图痕迹即可)
∠ABC(无需写画法,保留画图痕迹即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,如取款、上网等都需要密码,有一种利用“因式分解”产生的密码,方便记忆,原理是:如多项式![]() ,若
,若![]() ,
,![]() 时,则各因式的值为
时,则各因式的值为![]() ,
,![]() ,
,![]() ,于是把018162作为一个六位数的密码,对于多项式
,于是把018162作为一个六位数的密码,对于多项式![]() ,取
,取![]() ,
,![]() 时,用上述方法产生的密码是_________________.(写一个即可)
时,用上述方法产生的密码是_________________.(写一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.
(1)当t=5时, OP长为____________;
(2)当点P在BC边上时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com