
【题目】综合题
(1)如图1,△ABC中, ![]() ,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;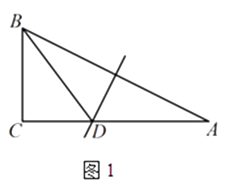
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求 ![]() 的度数;
的度数;
③若 ![]() ,则
,则 ![]() 的值为 .
的值为 . 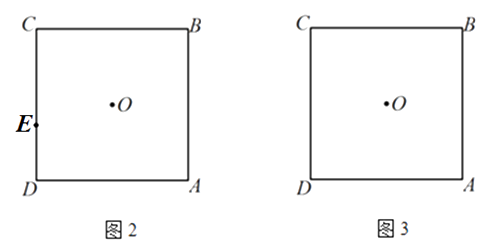
【答案】
(1)3
(2)解:①如图,△ ![]() 即为所求;
即为所求;  ,②在AD上截取AH,使得AH=DE,连接OA、OD、OH.
,②在AD上截取AH,使得AH=DE,连接OA、OD、OH. ∵点O为正方形ABCD的中心,∴
∵点O为正方形ABCD的中心,∴ ![]() ,
,![]() ,
,![]() .∴△
.∴△ ![]() ≌△
≌△ ![]() .∴
.∴ ![]() ,
,![]() .∴
.∴ ![]() .∵△
.∵△ ![]() 的周长等于
的周长等于 ![]() 的长,∴
的长,∴ ![]() .∴△
.∴△ ![]() ≌△
≌△ ![]() .∴
.∴ ![]() .,③
.,③ ![]() .
.
【解析】(1) ![]() AB的垂直平分线交AC于点D,
AB的垂直平分线交AC于点D,
∴BD=AD,
∴ ![]() BCD的周长=BC+CD+BD=BC+AC=1+2+3,
BCD的周长=BC+CD+BD=BC+AC=1+2+3,
所以答案是:3
( 2 )③作OG ![]() CD于G,OK
CD于G,OK ![]() AD于K,如图3所示:
AD于K,如图3所示:

设AF=8t,则CE=9t,设OG=m,
∵O为正方形ABVD的中心,
∴四边形OGDK为正方形,CG=DG=DK=KA= ![]() AB=OG,
AB=OG,
∴GE=CE-CG=9t-m,DE=2CG-CE=2m-9t,FK=AF-KA=8t-m,DF=2DK-AF=2m-8t,
由(2)②知 ![]() EOG ≌
EOG ≌ ![]() HOF,
HOF,
∴OE=OH,EF=FH,
在Rt ![]() EOG和Rt
EOG和Rt ![]() HOK中,
HOK中,
![]() ,
,
∴Rt ![]() EOG ≌Rt
EOG ≌Rt ![]() HOK(HL),
HOK(HL),
∴GE=KH,
∴EF=GE+FK=9t-m+8t-m=17t-2m,
由勾股定理得:DE2+DF2=EF2,
∴(2m-9t)2+(2m-8t)2=(17t-2m)2,
整理得:(m+6t)(m-6t)=0,
∴m=6t
∴OG=OK=6t,GE=9t-m=9t-6t=3t,FK=8t-m=2t,
∴ ![]()
所以答案是: ![]()
【考点精析】掌握比例的性质是解答本题的根本,需要知道基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一张边长为![]() 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工![]() (
(![]() 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为![]() ,请回答下列问题:
,请回答下列问题:
(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
(2)完成下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
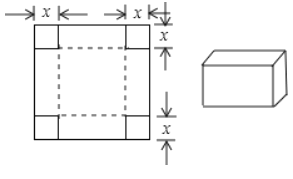
(3)观察上表,当![]() 取什么值时,容积
取什么值时,容积![]() 的值最大?
的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,定义直线
中,定义直线 ![]() 与双曲线
与双曲线 ![]() 的交点
的交点 ![]() (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 ![]() 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 ![]() 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.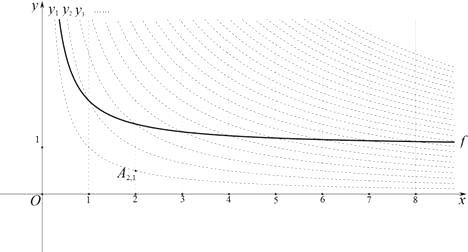
(1)①“双曲格点” ![]() 的坐标为;
的坐标为;
②若线段 ![]() 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线 ![]() 是双曲线
是双曲线 ![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 ![]() ,则
,则 ![]() 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线 ![]() 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 ![]() 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” ![]() 、
、 ![]() 、
、 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xoy中,一次函数y= ![]() x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.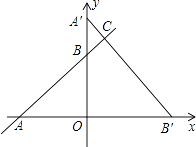
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(![]() -
-![]() +
+![]() )×36]÷5 (4)99
)×36]÷5 (4)99![]() ×(-36)
×(-36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.
(1)直尺的长为多少个单位长度(直接写答案)
(2)如图2,直尺AB在数轴上移动,有BC=4OA,求此时A点对应的数;
(3)如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2, 若t1﹣t2=2(秒),求直尺放入蓬内,A点对应的数为多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. 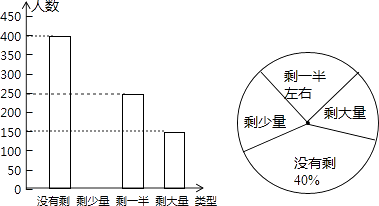
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com