
分析 先确定抛物线y=x2-1的顶点坐标为(0,-1)和抛物线y=x2-1与x轴的交点为(-1,0),(1,0),画出抛物线,然后把抛物线y=x2-1图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=-x2+1(-1≤x≤1),有图象可得当直线y=x+m过点A时,直线y=x+m与该新图象恰好有三个公共点,易得对应的m的值为1;当直线y=x+m与抛物线y=-x2+1(-1≤x≤1)相切时,直线y=x+m与该新图象恰好有三个公共点,即-x2+1=x+m有相等的实数解,利用根的判别式的意义可求出此时m的值,进而得到直线y=x+m与新图象有4个公共点时,m的取值范围.
解答 解:∵y=x2-1,
∴抛物线y=x2-1的顶点坐标为(0,-1),
当y=0时,x2-1=0,解得x1=-1,x2=1,则抛物线y=x2-1与x轴的交点为(-1,0),(1,0),
把抛物线y=x2-1图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=-x2+1(-1≤x≤1),
如图,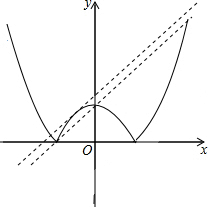
把直线y=x向上平移,当平移后的直线y=x+m过点A时,直线y=x+m与该新图象恰好有三个公共点,所以-1+m=0,解得m=1;
当直线y=x+m与抛物线y=-x2+1(-1≤x≤1)相切时,直线y=x+m与该新图象恰好有三个公共点,即-x2+1=x+m有相等的实数解,整理得x2+x+m-1=0,△=12-4(m-1)=0,解得m=$\frac{5}{4}$,
所以当直线y=x+m与新图象有4个公共点时,m的取值范围是1<m<$\frac{5}{4}$.
故答案为1<m<$\frac{5}{4}$.
点评 本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.


科目:初中数学 来源: 题型:选择题
 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )| A. | (6$\sqrt{3}$-$\frac{4}{3}$π)m2 | B. | (8$\sqrt{3}$-$\frac{4}{3}$π)m2 | C. | (6$\sqrt{3}$-$\frac{8}{3}$π)m2 | D. | (8$\sqrt{3}$-$\frac{8}{3}$π)m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.
如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
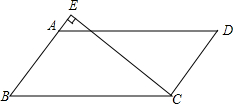 如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )| A. | 53° | B. | 37° | C. | 47° | D. | 123° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
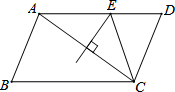 如图,在平行四边形ABCD中,AB=m,BC=n,AC的垂直平分线交AD于点E,则△CDE的周长是( )
如图,在平行四边形ABCD中,AB=m,BC=n,AC的垂直平分线交AD于点E,则△CDE的周长是( )| A. | m+n | B. | mn | C. | 2(m+n) | D. | 2(n-m) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com