
【题目】在⊙O中,![]() 的度数为120°,点P为弦AB上的一点,连结OP并延长交⊙O于点C,连结OB,AC.
的度数为120°,点P为弦AB上的一点,连结OP并延长交⊙O于点C,连结OB,AC.
(1)若P为AB中点,且PC=1,求圆的半径.
(2)若BP:BA=1:3,请求出tan∠OPA.
科目:初中数学 来源: 题型:
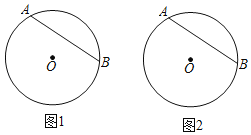
【题目】(1)问题背景:
如图1,在正方形ABCD中,点M,N分别在边BC,CD上,连接MN,且∠MAN=45°,将△ADN绕点A顺时针旋转90°,得到△ABG,可证△AMG≌△AMN,易得线段MN、BM、DN之间的数量关系为: (直接填写);
(2)实践应用:
在平面直角坐标系中,边长为5的正方形OABC的两顶点分别在y轴、x轴的正半轴上,O在原点.现将正方形OABC绕点O按顺时针方向旋转,旋转角为θ,当点A第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.如图2,设△MBN的周长为P,在旋转正方形OABC的过程中,P值是否有变化?请证明你的结论;
(3)拓展研究:
如图3,将正方形改为长与宽不相等的矩形,且∠MAN=∠CMN=45°,请你直接写出线段MN、BM、DN之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
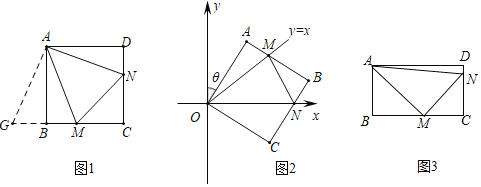
【题目】如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在![]() 中,直径
中,直径![]() ,
,![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() .
.

(Ⅰ)![]() 的度数为_________;(直接写出答案)
的度数为_________;(直接写出答案)
(Ⅱ)如图2,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的度数;
的度数;
(Ⅲ)如图3,弦![]() 与弦
与弦![]() 不相交,求
不相交,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() ,点
,点![]() 在
在![]() 轴上.
轴上.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 在第二象限内一点,直线
在第二象限内一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的解析式;
的解析式;
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() 、
、![]() 是
是![]() 延长线上的两点(点
延长线上的两点(点![]() 在点
在点![]() 的右侧),
的右侧),![]() ,连接
,连接![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:

(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN≌△OAD;④AN2+CM2=MN2;其中正确的结论是_____.(填写所有正确结论的序号)
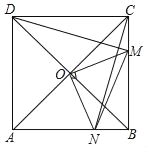
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究“尺规三等分角”这个数学名题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是( )
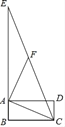
A. 7° B. 21° C. 23° D. 34°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 匀速运动.动点
匀速运动.动点![]() 同时从点
同时从点![]() 出发以同样的速度沿
出发以同样的速度沿![]() 的延长线方向匀速运动,当点
的延长线方向匀速运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 同时停止运动.设运动时间为以
同时停止运动.设运动时间为以![]() .过点
.过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 边于
边于![]() .以
.以![]() 为边作平行四边形
为边作平行四边形![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
(2)是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的平分线上?若存在,求出
的平分线上?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求![]() 的长;
的长;
(4)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,得
翻折,得![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的值最小?并求出最小值.
的值最小?并求出最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com