
【题目】下列命题中,真命题是( ).
(A)周长相等的锐角三角形都全等; (B) 周长相等的直角三角形都全等;
(C)周长相等的钝角三角形都全等; (D) 周长相等的等腰直角三角形都全等.
科目:初中数学 来源: 题型:
【题目】小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( ) 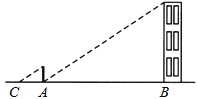
A.10米
B.12米
C.15米
D.22.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)“六·一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩
具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5
倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足同学们课外阅读的需求,某中学图书馆向出版社邮购科普系列图书,每本书单价为16元,书的价钱和邮费是通过邮局汇款,相关的书价折扣、邮费和汇款的汇费如下表所示(总费用=总书价+总邮费+总汇费)
购书数量 | 折扣 | 邮费 | 汇费 |
不超过10本 | 九折 | 6元 | 每100元汇款需汇费1元 (汇款不足100元时按100元汇款收汇费) |
超过10本 | 八折 | 总书价的10% | 每100元汇款需汇费1元 (汇款不足100元的部分不收汇费) |
(1)若一次邮购7本,共需总费用为 元.
(2)已知学校图书馆需购图书的总数是10的整倍数,且超过10本.
①若分次邮购,分别汇款,每次邮购10本,总费用为1064元时,共邮购了多本图书?
②若你是学校图书馆负责人,从节约的角度出发,在“每次邮购10本“与“一次性邮购”这两种方式中选择一种,你会选择哪一种?计算并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率= | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近多少?(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)是多少?
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
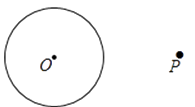
小敏的作法如下:
如图,
①链接op,做线段op的垂直平分线MN,交OP于点C
②以点C为圆心,CO的长为半径作圆,交⊙O于A、B两点
③作直线PA、PB所以直线PA,PB就是所求的切线
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,且AB= ![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA. 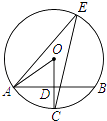
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为 ![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
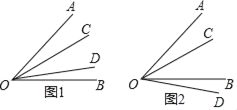
【题目】回答问题:
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=![]() ∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=
∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=![]() ∠AOC,如图1和图2所示,求∠COD的度数.
∠AOC,如图1和图2所示,求∠COD的度数.
(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=![]() CB,点D是直线AB上满足BD=
CB,点D是直线AB上满足BD=![]() AC.请画出示意图,求出线段CD的长.
AC.请画出示意图,求出线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com