如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
 |
科目：初中数学 来源： 题型：
小明在学习轴对称的时候，老师留了这样一道思考题
：如图，已知在直线l的同侧有A、B两点，请你在直线l上确定一点P，使得PA+PB的值最小.小明通过独立思考，很快得出了
解决这个问题的正确方法，他的作法是这样的：
①作点A关于直线l的对称点A′.②连结A′B，交直线l于点P.则点P为所求.
请你参考小明的作法解决下列问题：
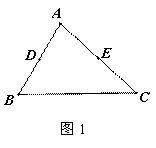
（1）如图1，在△ABC中，点D、E分别是AB、AC边的中点，BC=6，BC边上的高为4，请你在BC边上确定一点P，使得△PDE的周长最小.
①在图1中画出点P.（三角板、刻度尺画图，保留画图痕迹，不写画法）
②请直接写出△PDE周长的最小值 .
（2）如图2在矩形ABCD中，AB=4，BC=6，G为边AD的中点，若E、F为边AB上的两个动点，点E在点F左侧，且EF=1，当四边形CGEF的周长最小时，请你在图2中确定点E、F的位置.（三角板、刻度尺画图，保留画图痕迹，不写画法），并直接写出四边形CGEF周长的最小值 .
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G，
（1）完成下面的证明：
∵ MG平分∠BMN（ ），
∴ ∠GMN＝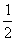
∠BMN（ ），
同理∠G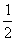NM＝∠DNM．
∵ AB∥CD（ ），
∴ ∠BMN＋∠DNM＝________（ ）．
∴ ∠GMN＋∠GNM＝________．
∵ ∠GMN＋∠GNM＋∠G＝________（ ），
∴ ∠G＝ ________．
∴ MG与NG的位置关系是________．
（2）把上面的题设和结论，用文字语言概括为一个命题：
_______________________________________________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图：AB∥CD，GO和HO分别是∠BGH和∠GHD的角平分线。你能算出∠GOH的度数吗？如果作OP⊥AB，OQ⊥CD，OR⊥EF，你能找到图中的全等三角形吗？说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图2，在正方形ABCD中，E为DC边上的点，连接BE，将△BCE绕点C顺时针方向旋转90°得到△DCF，连接EF，若∠BEC＝60°，则∠EFD的度数为（ ）
图2
A.10° B.15° C.20° D.25°
查看答案和解析>>
科目：初中数学 来源： 题型：
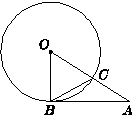
如图1，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO=40°，则∠OCB的度数为（ ）
A．40° B．50° C．65° D．75°
查看答案和解析>>
科目：初中数学 来源： 题型：
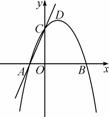
综合与探究：如图，在平面直角坐标系中，抛物线y＝－x2＋2x＋3与x轴交于A、B两点，与y轴交于点C，点
D是该抛物线的顶点．
(1)求直线AC的解析式及B、D两点的坐标；
(2)点P是x轴上一个动点，过P作直线l∥AC交抛物线于点Q.试探究：随着P点的运动，在抛物线上是否存在点Q，使以点A、P、Q、C为顶点的四边形是平行四边形，若存在，请直接写出符合条件的点Q的坐标；若不存在，请说明理由；
(3
)请在直线AC上找一点M，使△BDM的周长最小，求出M点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
