
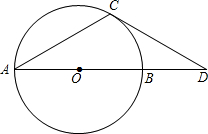
 如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.
如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.分析 (1)已知点C在⊙O上,先连接OC,由已知CA=CD,∠CDA=30°,得∠CAO=30°,∠ACO=30°所以得到∠COD=60,根据三角形内角和定理得∠DCO=90°即能判断直线CD与⊙O的位置关系.
(2)要求点A到CD所在直线的距离,先作作AE⊥CD,垂足为E,由∠CDA=30°,得AE=$\frac{1}{2}$AD,在直角三角形OCD中,半径OD=6,所以OD=2OC=12,AD=OA+0D=18.从而求出AE.
解答 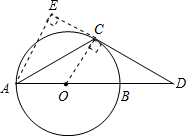 解:(1)∵△ACD是等腰三角形,∠D=30°,
解:(1)∵△ACD是等腰三角形,∠D=30°,
∴∠CAD=∠CDA=30°.
连接OC,
∵AO=CO,
∴△AOC是等腰三角形,
∴∠CAO=∠ACO=30°,
∴∠COD=60°,
在△COD中,又∵∠CDO=30°,
∴∠DCO=90°
∴CD是⊙O的切线,即直线CD与⊙O相切.
(2)过点A作AE⊥CD,垂足为E.
在Rt△COD中,∵∠CDO=30°,
∴OD=2OC=12,
AD=AO+OD=6+12=18,
在Rt△ADE中,
∵∠EDA=30°,
∴点A到CD边的距离为:AE=$\frac{AD}{2}$=9.
点评 此题考查的知识点是切线的判定与性质,解题的关键是运用直角三角形的性质及30°角所对直角边的性质,三角形内角和定理.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
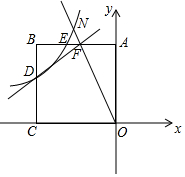 如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE.
如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-x-1=x(x-1)-1 | B. | a2-ab=a(a-b) | C. | x2-1=x(x-$\frac{1}{x}$) | D. | (x+2)(x-2)=x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
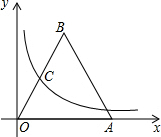 如图,等边三角形OAB的一边OA在x轴上,双曲线y=$\frac{\sqrt{3}}{x}$在第一象限内的图象经过OB边的中点C,则点B的坐标是(2,2$\sqrt{3}$).
如图,等边三角形OAB的一边OA在x轴上,双曲线y=$\frac{\sqrt{3}}{x}$在第一象限内的图象经过OB边的中点C,则点B的坐标是(2,2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源:2017届山东省济宁市阶段教育学校统一招生考试数学模拟试卷(解析版) 题型:解答题
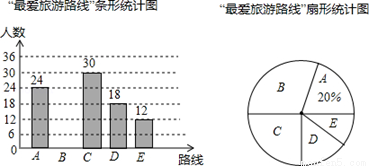
2016年5月9日﹣11日,贵州省第十一届旅游产业发展大会在准一市茅台镇举行,大会推出五条遵义精品旅游线路:A红色经典,B醉美丹霞,C生态茶海,D民族风情,E避暑休闲.某校摄影小社团在“祖国好、家乡美”主题宣传周里,随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条心中最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图,请解决下列问题.
(1)本次参与投票的总人数是 人.
(2)请补全条形统计图.
(3)扇形统计图中,线路D部分的圆心角是 度.
(4)全校2400名学生中,请你估计,选择“生态茶海”路线的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com