

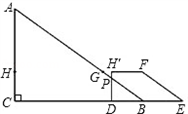
| 解:(1)∵AH:AC=2:3,AC=6 ∴AH=  AC= AC= ×6=4 ×6=4又∵HF∥DE, ∴HG∥CB,∴△AHG∽△ACB ∴  = =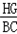 ,即 ,即 = = , ,∴HG= 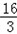 ∴S△AHG= ∴S△AHG= AH*HG= AH*HG= ×4× ×4×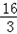 = =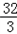 . .(2)①能为正方形 ∵HH′∥CD,HC∥H′D, ∴四边形CDH′H为平行四边形 又∠C=90°, ∴四边形CDH?H为矩形 又CH=AC﹣AH=6﹣4=2 ∴当CD=CH=2时, 四边形CDH′H为正方形 此时可得t=2秒时,四边形CDH?H为正方形. ②(Ⅰ)∵∠DEF=∠ABC, ∴EF∥AB ∴当t=4秒时,直角梯形的腰EF与BA重合. 当0≦t≦4时,重叠部分的面积为直角梯形DEFH′的面积. 过F作FM⊥DE于M,  =tan∠DEF=tan∠ABC= =tan∠DEF=tan∠ABC=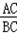 = = = = ∴ME=  FM= FM= ×2= ×2= ,HF=DM=DE﹣ME=4﹣ ,HF=DM=DE﹣ME=4﹣ = = ∴直角梯形DEFH′的面积为  (4+ (4+ )×2= )×2=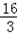 ∴y= 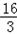 . .(Ⅱ)∵当4<t≦5  时,重叠部分的面积为四边形CBGH的面积一矩形CDH?H的面积. 时,重叠部分的面积为四边形CBGH的面积一矩形CDH?H的面积.而S四边形CBGH=S△ABC﹣S△AHG=  ×8×6﹣ ×8×6﹣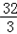 = =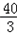 S矩形CDH′H=2t ∴y= 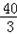 ﹣2t. ﹣2t.(Ⅲ)当5  <t≦8时,如图,设H′D交AB于P,BD=8﹣t <t≦8时,如图,设H′D交AB于P,BD=8﹣t又  =tan∠ABC= =tan∠ABC= ∴PD=  DB= DB= (8﹣t) (8﹣t)∴重叠部分的面积y=S △PDB=  PD×DB= PD×DB=  (8﹣t)(8﹣t)= (8﹣t)(8﹣t)= (8﹣t)2= (8﹣t)2= t2﹣6t+24. t2﹣6t+24.∴重叠部分面积y与t的函数关系式: y= 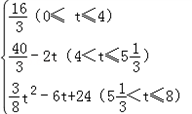 . . |
 |


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com