
分析 (1)设购买一块A型小黑板需要x元,一块B型为(x-20)元,根据,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元可列方程求解.
(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块,根据需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的$\frac{1}{3}$,可列不等式组求解.
解答 解:(1)设购买一块A型小黑板需要x元,一块B型为(x-20)元,
5x+4(x-20)=820,
x=100,
x-20=80,
购买A型100元,B型80元;
(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块,
$\left\{\begin{array}{l}{100m+80(60-m)≤5240}\\{m>60×\frac{1}{3}}\end{array}\right.$,
∴20<m≤22,
而m为整数,所以m为21或22.
当m=21时,60-m=39;
当m=22时,60-m=38.
所以有两种购买方案:方案一购买A21块,B 39块、
方案二 购买A22块,B38块
点评 本题考查理解题意的能力,关键根据购买黑板块数不同钱数的不同求出购买黑板的钱数,然后要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的$\frac{1}{3}$,列出不等式组求解.


科目:初中数学 来源: 题型:解答题
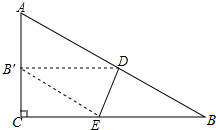 如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.
如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤3 | B. | m≥3 | C. | m>3 | D. | m<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
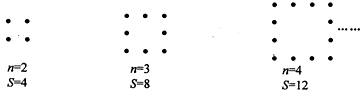
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=(x-2)(x+3)+1 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com