



 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
| 2 |
| A、方程有两个不相等的实数根 |
| B、方程有两个相等的实数根 |
| C、方程没有实数根 |
| D、方程根的情况不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC中,∠C=90°,AC=BC=2
如图,已知△ABC中,∠C=90°,AC=BC=2| 2 |
A、2-
| ||||
B、
| ||||
C、2(
| ||||
| D、1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
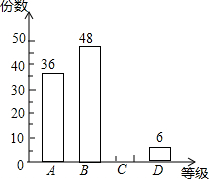 某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.查看答案和解析>>
科目:初中数学 来源: 题型:
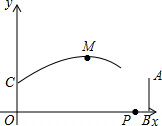 在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.
在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com