
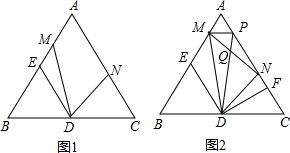
 连DM,作DN平分∠MDC交AC于N.
连DM,作DN平分∠MDC交AC于N.| PQ |
| QD |
| MP |
| DK |
| 2 |
| 7 |
| 2 |
| 9 |
 (1)证明:延长AC至M′,使CM′=EM,连接DM′,
(1)证明:延长AC至M′,使CM′=EM,连接DM′,| 1 |
| 2 |
| 1 |
| 2 |
|
| 3 |
| 3 |

| 3 |
| MR |
| FN |
| RN |
| DF |
|
| PQ |
| QD |
| MP |
| DK |
| 2 |
| 7 |
| 2 |
| 9 |
| 2 |
| 9 |
| 28 |
| 9 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
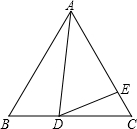 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com