“共建环保模范城,共享绿色新重庆”,市政府强力推进城市生活污水处理、生活垃圾处理设施建设改造工作.为此,某化工厂在一期工程完成后购买了4台甲型和5台乙型污水处理设备,共花费资金102万元,且每台乙型设备的价格比每台甲型设备价格少3万元.已知每台甲型设备每月能处理污水240吨,每台乙型设备每月能处理污水180吨.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共12台用于二期工程的污水处理,预算本次购买资金不超过129万元,预计二期工程完成后每月将产生不少于2220吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少万元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)请你说明在(2)的所有方案中,哪种购买方案的总花费最少?
解:(1)设每台甲型设备是x万元,每台乙型设备的价格是y万元,根据题意得:
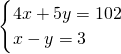
,
解得:
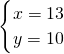
.
答:每台甲型设备是13万元,每台乙型设备的价格是10万元.
(2)设购买甲型设备a(a为整数)台,乙型设备(12-a)台,根据题意得:
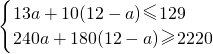
,
解得:1≤a≤3,
∵a为整数,
∴a=,1,2,3.
∴购买方案有:①、甲型1台,乙型11台;
②、甲型2台,乙型10台;
③、甲型3台,乙型9台.
(3)方案①的费用为:1×13+11×10=123万元;
方案②的费用为:2×13+10×10=126万元;
方案③的费用为:3×13+9×10=129万元.
∵123<126<129,
∴方案①总花费最少.
分析:(1)设每台甲型设备是x万元,每台乙型设备的价格是y万元,根据题意列出方程就可以求出其解.
(2)设购买甲型设备a台,乙型设备(12-a)台,根据题意可以建立不等式组,从而求出其解.
(3)分别计算出各种方案的费用,就可以比较出最少方案的花费.
点评:本题考查了二元一次方程组的解法及运用,一元一次不等式组的解法及运用,方案设计问题的解答,在解答中注意未知数在题目中的隐含条件的运用.

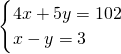 ,
,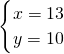 .
.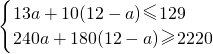 ,
,
