
分析 先把x化简,根据$1<\sqrt{2}<2$,所以$2<\sqrt{2}+1<3$,再确定m、n的值,即可解答.
解答 解:x=$\frac{1}{\sqrt{2}-1}$=$\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}=\sqrt{2}+1$,
∵$1<\sqrt{2}<2$,
∴$2<\sqrt{2}+1<3$,
∴m=$\sqrt{2}+1-2=\sqrt{2}-1$,
-x=-$\sqrt{2}-1$,可以画一条数轴去直观的确定n=2-$\sqrt{2}$
∵$2<\sqrt{2}+1<3$,
∴$-3<-\sqrt{2}-1<-2$,
∴n=$-\sqrt{2}-1+2$=1-$\sqrt{2}$,
∴m3+n3+3mn=$(\sqrt{2}-1)^{3}$+$(1-\sqrt{2})^{3}$+3($\sqrt{2}$-1)(1$-\sqrt{2}$)=3-6$\sqrt{2}$
故答案为:3-6$\sqrt{2}$.
点评 本题考查了估算无理数的大小,解决本题的关键是估算$\sqrt{2}$的大小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点D为线段AB延长线上一点,△ABC和△BDE分别是以AB,BD为斜边的等腰直角三角形.连接CE并延长,交AD的延长线于F,△ABC的外接圆圆O交CF与点M.若AB=6,BD=2.
如图,点D为线段AB延长线上一点,△ABC和△BDE分别是以AB,BD为斜边的等腰直角三角形.连接CE并延长,交AD的延长线于F,△ABC的外接圆圆O交CF与点M.若AB=6,BD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
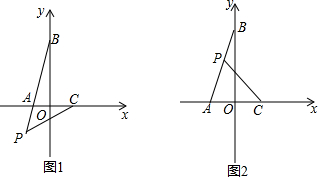
 甲乙两车分别从A、B两地同时出发,相向而行,甲车以m千米/时的速度从A地匀速驶往B地,到达B地后停留在B地;乙车以n千米/时的速度从B地匀速驶往A地,到达A地后,立即以2n千米/时的速度沿原路匀速返回B地,设两车相距y(千米),乙车行驶时间为t(时),两车从出发至乙车到达A地过程中y与t的图象如图所示.
甲乙两车分别从A、B两地同时出发,相向而行,甲车以m千米/时的速度从A地匀速驶往B地,到达B地后停留在B地;乙车以n千米/时的速度从B地匀速驶往A地,到达A地后,立即以2n千米/时的速度沿原路匀速返回B地,设两车相距y(千米),乙车行驶时间为t(时),两车从出发至乙车到达A地过程中y与t的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
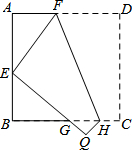 如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )
如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com