
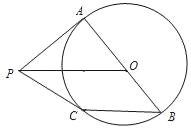
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
【答案】(1)PC是⊙O的切线,理由见解析;(2)![]()
【解析】试题分析:(1)要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.
(2)可以连接AC,根据已知先证明△ACB∽△PCO,再根据勾股定理和相似三角形的性质求出PC的长.
试题解析:(1)结论:PC是⊙O的切线.
证明:连接OC
∵CB∥PO
∴∠POA=∠B,∠POC=∠OCB
∵OC=OB
∴∠OCB=∠B
∴∠POA=∠POC
又∵OA=OC,OP=OP
∴△APO≌△CPO
∴∠OAP=∠OCP
∵PA是⊙O的切线
∴∠OAP=90°
∴∠OCP=90°
∴PC是⊙O的切线.

(2)连接AC
∵AB是⊙O的直径
∴∠ACB=90°(6分)
由(1)知∠PCO=90°,∠B=∠OCB=∠POC
∵∠ACB=∠PCO
∴△ACB∽△PCO
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,m),B(n,3)两点,一次函数
的图象交于A(1,m),B(n,3)两点,一次函数![]() 的图象与y轴交于点C.
的图象与y轴交于点C.
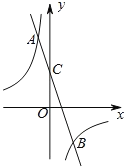
(1)求一次函数的解析式;
(2)点P是x轴上一点,且△BOP的面积是△BOC面积的2倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
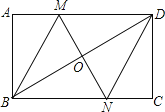
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )种
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑”.记,![]()
![]() ,
,![]() .
.
同学们,通过以上材料的阅读,请回答下列问题:
(1)计算(填写最后的结果)
![]() =__________;
=__________;![]() ____________.
____________.
(2)2+4+6+8+10用求和公式符号可表示为__________.
(3)化简:![]()
(4)若对于任意x都存在![]() ,请求代数式
,请求代数式![]() b-ab的值.
b-ab的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
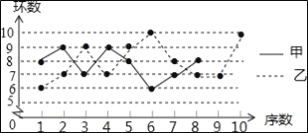
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是_____,中位数是______.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
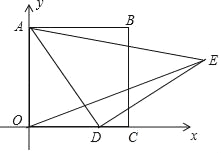
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )
A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式![]() x2y4的次数为c.
x2y4的次数为c.
![]()
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com